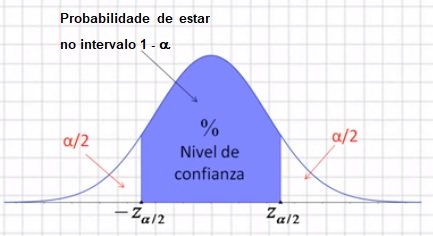
Intervalo de confianza para a media
Se temos unha poboación que segue unha distribución normal \(N(\mu, \sigma)\). Non coñecemos o valor da media da poboación, pero si o da desviación típica. Se nesta poboación seleccionamos unha mostra de tamaño \(n\) con media mostral \(\overline{x}\), podemos estimar, cun nivel de confianza \(1 - \alpha\), a media da poboación mediante o seguinte intervalo:
\[\displaystyle \left(\overline{x} - \frac{\sigma}{\sqrt{n}} z_{\alpha/2}, \overline{x} + \frac{\sigma}{\sqrt{n}} z_{\alpha/2}\right)\]
Isto quere dicir que se cumprirá que \(\displaystyle \overline{x} - \frac{\sigma}{\sqrt{n}} z_{\alpha/2} < \mu < \overline{x} + \frac{\sigma}{\sqrt{n}} z_{\alpha/2}\) cunha confianza de \(1 - \alpha\).
O peso das bicas que fan nunha determinada panadería seguen unha distribución normal de desviación típica 10 gramos. Nunha mostra aleatoria de 64 bicas obtivemos que a masa media era de 502 gramos. Atopa o intervalo de confianza do 95% para o peso medio de todas as bicas.
Os datos que temos son:
- \(\sigma = 10\)
- \(n = 64\)
- \(\overline{x} = 502\)
- \(\displaystyle 1 - \alpha = 0,95 \implies \alpha = 0,05 \implies \frac{\alpha}{2} = 0,025 \rightarrow P(Z < z_{\alpha/2}) = 0,975 \implies z_{\alpha/2} = 1,96\)
Polo tanto o intervalo de confianza para a media será:
\(\displaystyle \left(502 - \frac{10}{\sqrt{64}} \cdot 1,96, 502 + \frac{10}{\sqrt{64}} \cdot 1,96\right) = (502 - 2,45, 502 + 2,45) = (499,55, 504,45)\)
É dicir, podemos asegurar cunha confianza do 95% que o peso medio de todas as bicas estará entre 499,55 e 504,45 gramos.
Intervalo de confianza para a proporción
Nunha poboación chamaremos \(p\) á proporción de individuos que teñen certa característica. Se nesta poboación seleccionamos unha mostra de tamaño \(n\) e sendo \(\hat{p}\) a proporción desa característica para a mostra, podemos estimar, cun nivel de confianza \(1 - \alpha\), a proporción da poboación mediante o seguinte intervalo:
\[\displaystyle \left(\hat{p} - \sqrt{\frac{\hat{p}(1 - \hat{p})}{n}} z_{\alpha/2}, \hat{p} + \sqrt{\frac{\hat{p}(1 - \hat{p})}{n}} z_{\alpha/2}\right)\]
Isto quere dicir que se cumprirá que \(\displaystyle \hat{p} - \sqrt{\frac{\hat{p}(1 - \hat{p})}{n}} z_{\alpha/2} < p < \hat{p} + \sqrt{\frac{\hat{p}(1 - \hat{p})}{n}} z_{\alpha/2}\) cunha confianza de \(1 - \alpha\).
Un fabricante de medicamentos afirma que certa medicina cura unha enfermidade. Os inspectores de sanidade utilizan o medicamento nunha mostra de 100 pacientes e observan que funciona en 85 casos. Indica, cun nivel de confianza do 90%, un intervalo de confianza para a proporción de persoas que poden curar usando dito medicamento.
Os datos que temos son:
- \(\displaystyle \hat{p} = \frac{85}{100}\)
- \(n = 100\)
- \(\displaystyle 1 - \alpha = 0,90 \implies \alpha = 0,10 \implies \frac{\alpha}{2} = 0,05 \rightarrow P(Z < z_{\alpha/2}) = 0,95 \implies z_{\alpha/2} = 1,645\)
Polo tanto o intervalo de confianza para a media será:
\(\displaystyle \left(0,85 - \sqrt{\frac{0,85 \cdot (1 - 0,85)}{100}} \cdot 1,645, 0,85 - \sqrt{\frac{0,85 \cdot (1 - 0,85)}{100}} \cdot 1,645\right) = (0,85 - 0,059, 0,85 + 0,059) = (0,791, 0,909)\)
É dicir, podemos asegurar cunha confianza do 90% que o medicamento funciona entre o 79,1% e o 90,9% dos casos.