Área encerrada por unha curva
No caso que a función \(f(x)\), continua en \([a, b]\) non teña cortes co eixe \(X\) en dito intervalo, o valor absoluto da integral definida \(\displaystyle \int_{a}^{b} f(x) dx\) correspóndese coa área no recinto limitado pola curva \(y = f(x)\) e o eixe de abscisas no intervalo \([a, b]\).
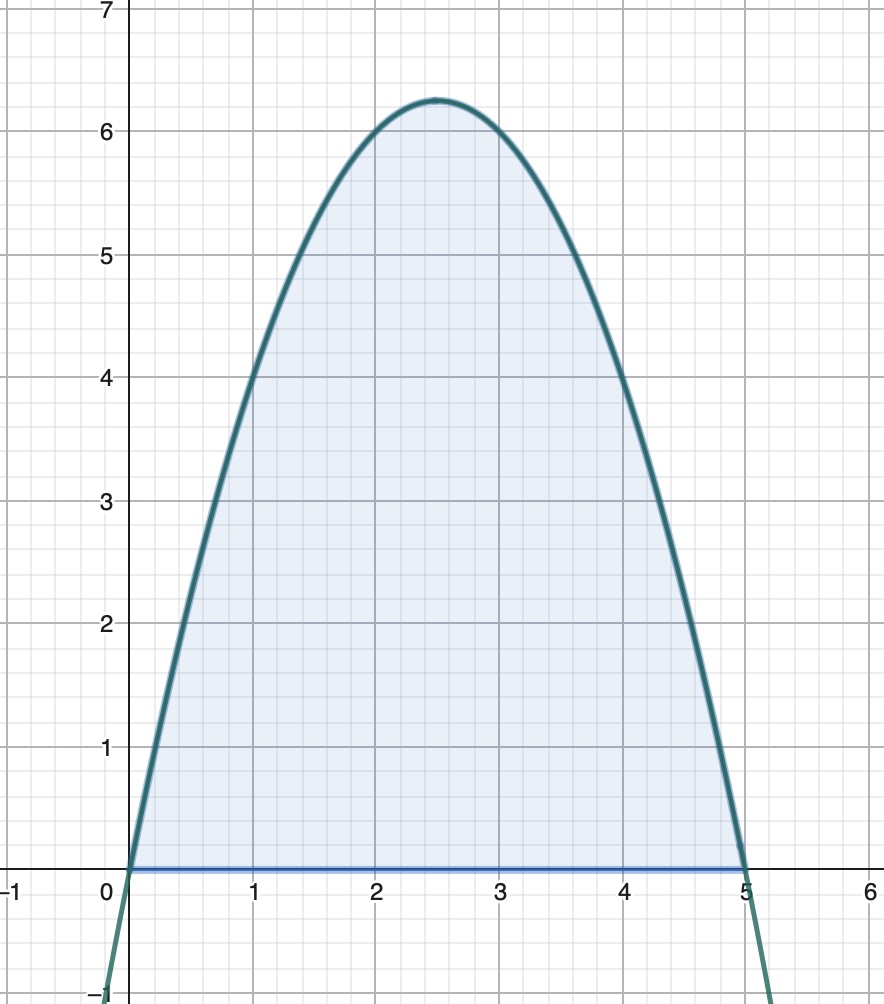
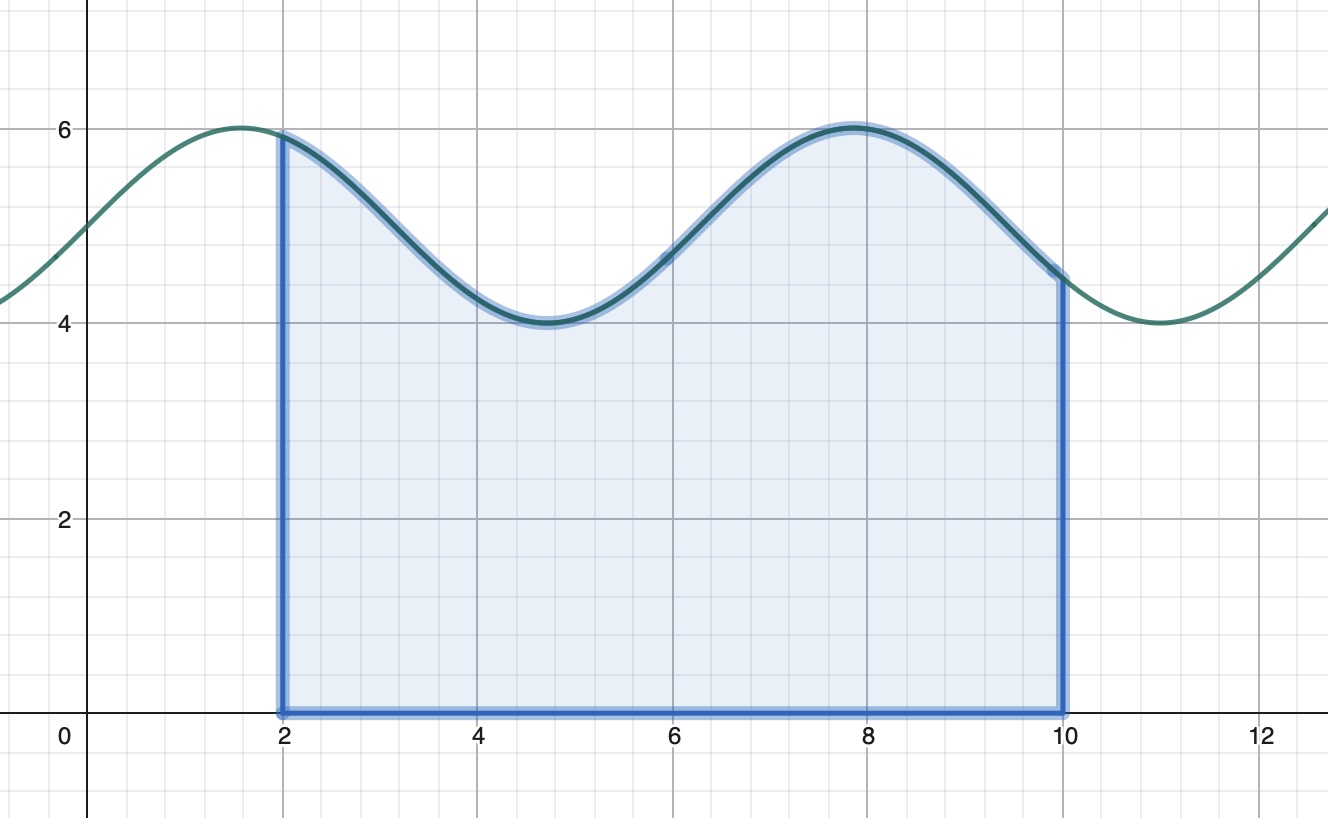
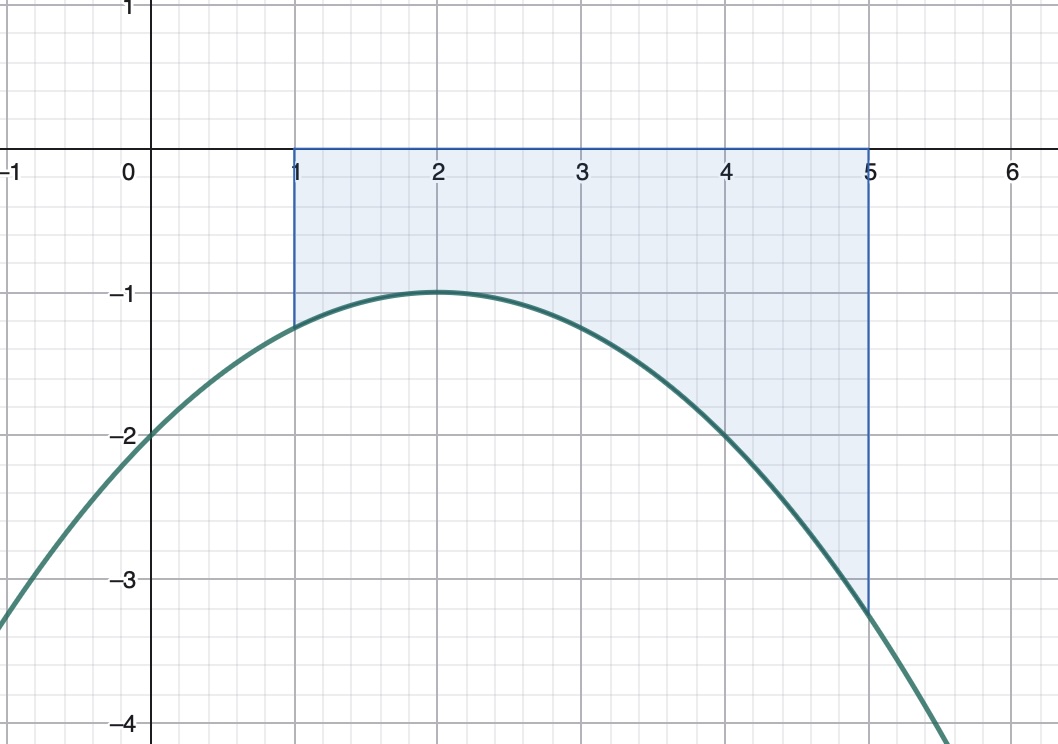
Nestes casos Área \(\displaystyle = \left| \int_{a}^{b} f(x) dx \right|\).
No caso de que a curva corte ao eixe \(X\) dentro dos límites da integración, debemos dividir a integral en varias partes e ir considerando o valor absoluto de cada unha desas partes.
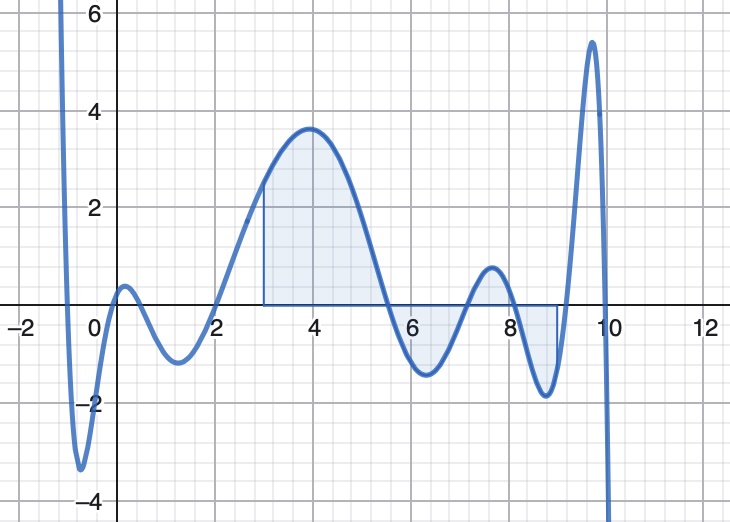
Neste último caso teríamos Área \(\displaystyle = \left| \int_{a}^{c1} f(x) dx \right| + \left| \int_{c1}^{c2} f(x) dx \right| + \left| \int_{c2}^{c3} f(x) dx \right| + \left| \int_{c3}^{b} f(x) dx \right|\), sendo \(c1, c2, c3\) os puntos de corte co eixe X de esquerda a dereita.
Pasos a dar para facer os exercicios:
1.- Calcular os puntos de corte co eixe \(X\). Para elo \(f(x) = 0\) e resólvese a ecuación resultante.
2.- Escribir a integral indicando os límites da integral definida.
3.- Calcular as integrais definidas que temos usando a regra de Barrow.
4.- Unha vez feitas as operacións terás un número, recorda que estabas a calcular un área, logo ese número será un número de unidades cadradas, de xeito que de non indicar en que unidade de lonxitude estamos traballando, ao final do exercicio se indicará o número seguido de \(u^2\), para indicar que se trata dunha cantidade que representa unha superficie.
Calcula a área limitada pola función \(f(x) = x(x + 2) \), as rectas \(x = -1\), \(x = 1\) e o eixe \(X\).
Calculamos os puntos de corte co eixe \(X\) da función: \(f(x) = x(x + 2) = 0 \implies x = 0, x = -2\).
Para a rexión da que temos que calcular a área so nos afecta o corte en \(x = 0\), logo para saber a área temos que calcular a seguinte integral:
\(\displaystyle \left|\int_{-1}^0 f(x) dx\right| + \left|\int_{0}^1 f(x) dx\right| = \left|\int_{-1}^0 x(x + 2) dx\right| + \left|\int_{0}^1 x(x + 2) dx\right| = \left|\int_{-1}^0 (x^2 + 2x) dx\right| + \left|\int_{0}^1 (x^2 + 2x) dx\right| = \)
\(\displaystyle = \left| \left.\frac{x^3}{3} + x^2\right]_{-1}^0 \right| + \left| \left.\frac{x^3}{3} + x^2\right]_{0}^1 \right| = \left| \frac{0^3}{3} + 0^2 - \left( \frac{(-1)^3}{3} + (-1)^2\right) \right| + \left| \frac{1^3}{3} + 1^2 - \left( \frac{0^3}{3} + 0^2\right) \right| =\)
\(\displaystyle= \left| -\frac{-1}{3} - 1\right| + \left| \frac{1}{3} + 1\right| = \left|\frac{-2}{3}\right| + \left|\frac{4}{3}\right| = 2 u^2\)