... E agora que?

Ordinaria 2023

Nunha cidade, o 70 % da poboación recibe publicidade dun establecemento, dos cales un 90 % realiza algunha compra en devandito establecemento. Tamén se sabe que dos que non reciben publicidade, un 60 % realiza algunha compra en devandito establecemento.

a) Que porcentaxe da poboación da cidade realiza algunha compra nese establecemento?

b) Se eliximos unha persoa ao azar que realizou algunha compra nese establecemento, cal é a probabilidade de que recibise publicidade do mesmo?

c) Son independentes os sucesos “realizar algunha compra nese establecemento” e “recibir publicidade do mesmo”? Xustifique a resposta.

Solución

a) Para calcular a probabilidade de que compre, facemos uso do teorema das probabilidades totais. Sendo \(C\) o suceso "compra no establecemento" e \(RP\) o suceso "recibe publicidade", temos:

    \(P(C) = P(C|RP) \cdot P(RP) + P(C|\overline{RP}) \cdot P(\overline{RP}) = 0,9 \cdot 0,7 + 0,6 \cdot 0,3 = 0,81\)

    A probabilidade de que unha persoa escollida ao chou compre na tenda é do 81 %.

b) Agora temos de condicionante que fixo algunha compra no establecemento, imos usar o teorema de Bayes para resolver este apartado.

    \(\displaystyle P(RP|C) = \frac{P(C|RP) \cdot P(RP)}{P(C)} = \frac{0,9 \cdot 0,7}{0,81} = 0,78\)

    A probabilidade de que unha persoa que compra no establecemento sexa unha persoa que recibiu a publicidade é do 78%.

c) Cando dous sucesos son independentes cúmprese que: \(P(C \cap RP) = P(C) \cdot P(RP)\).

    Imos ver que ocorre neste caso: \(P(C \cap RP) = P(C|RP) \cdot P(RP) = 0,9 \cdot 0,7 = 0,63\) e \(P(C) \cdot P(RP) = 0,81 \cdot 0,7 = 0,567\)

   Posto que \(P(C \cap RP) \neq P(C) \cdot P(RP)\), os sucesos non son independentes.

Extraordinaria 2023

Nunha urna A hai 8 bolas verdes e 6 vermellas e noutra urna B hai 4 verdes e 5 vermellas. Lánzase un dado e se sae un número menor que 3 sácase unha bola da urna A e se sae un número maior ou igual a 3 sácase a bola da urna B. Extráese unha bola o chou:

a) Calcule a probabilidade de que a bola extraída sexa vermella.

b) Sabendo que se extraeu unha bola verde, cal é a probabilidade de que saíra da urna A?

c) Son independentes os sucesos “extraer bola vermella” e “a bola procede da urna A “?

Solución

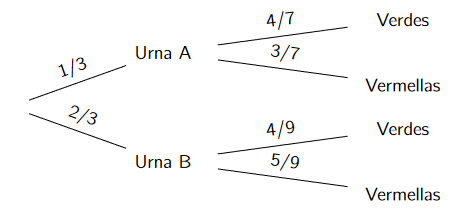
a) Para calcular a probabilidade de que sexa vermella, facemos uso do teorema das probabilidades totais.

    \(\displaystyle P(\text{Vermella}) = P(\text{Vermella}|A) \cdot P(A) + P(\text{Vermella}|B) \cdot P(B) = \frac{3}{7} \cdot \frac{1}{3} + \frac{5}{9} \cdot \frac{2}{3} = \frac{1}{7} + \frac{10}{27} = 0,51\)

    A probabilidade de que a bola extraída sexa vermella é de 0,51.

b) Neste caso o condicionamento ven dado por ser verde, imos usar o teorema de Bayes para calcular a probabilidade pedida, pero antes imos calcular a probabilidade de ser verde.

    \(P(\text{Verde}) = 1 - P(\text{Vermella}) = 1 - 0,51 = 0,49\)

    \(\displaystyle P(A|\text{Verde}) = \frac{P(\text{Verde}|A) \cdot P(A)}{P(\text{Verde})} = \frac{4/7 \cdot 1/3}{0,51} = 0,37\)

    A probabilidade de que tendo unha bola verde fora extraída da urna A é de 0,37.

c) Para que sexan independentes tense que cumprir:    \(P(\text{Vermella} \cap A) = P(\text{Vermella}) \cdot P(A)\)

   Imos comprobalo:

   \(\displaystyle P(\text{Vermella} \cap A) = P(\text{Vermella}|A) \cdot P(A) = \frac{3}{7} \cdot \frac{1}{3} = \frac{1}{7} = 0,14\)

   \(\displaystyle P(\text{Vermella}) \cdot P(A) = 0,51 \cdot \frac{1}{3} = 0,17\)

   Como non son iguais, os sucesos non son independentes.

Ordinaria 2022

Un estudo revela que 2 de cada 5 habitantes dunha determinada poboación son menores de 30 anos, o 70 % dos habitantes realizan exercicio físico con regularidade e o 30 % dos habitantes son menores de 30 anos e realizan exercicio físico con regularidade.

a) Que porcentaxe da poboación nin é menor de 30 anos nin realiza exercicio físico con regularidade?

b) Cal é a probabilidade de que un habitante que non realiza exercicio físico con regularidade sexa menor de 30 anos?

c) Son independentes os sucesos ser menor de 30 anos e realizar exercicio físico con regularidade? Xustifique a resposta.

Solución

Sexa \(A\) = {ser menor de 30 anos}, \(B\) = {realizan exercicio físico}, segundo o enunciado temos: \(\displaystyle P(A) = \frac{2}{5} = 0,4\), \(P(B) = 0,7\) e \(P(A \cap B) = 0,3\)

 a) Que non sexa menor de 30 e que non realice exercicio físico é o suceso \(\overline{A} \cap \overline{B}\)

    Polas leis de Morgan temos: \P(\overline{A} \cap \overline{B}) = P(\overline{A \cup B})\)

    \(P(\overline{A \cup B}) = 1 - P(A \cup B) = 1 - (P(A) + P(B) - P(A \cap B)) = 1 - (0,4 + 0,7 - 0,3) = 0,2\)

    Logo a poboación que non é menor de 30 e non realiza exercicio físico é do 20%.

b) Agora temos a condición de que non realiza exercicio físico e pide \(P(A|\overline{B})\)

    Pola definición de probabilidade condicionada: \(\displaystyle P(A|\overline{B}) = \frac{P(A \cap \overline{B})}{P(\overline{B})}\)

    \(P(A \cap \overline{B}) = P(A - B) = P(A) - P(A \cap B)\)

    Logo: \(\displaystyle P(A|\overline{B}) = \frac{P(A \cap \overline{B})}{P(\overline{B})} = \frac{P(A) - P(A \cap B)}{1 - P(B)} = \frac{0,4 - 0,3}{1 - 0,7} = 0,33\)

   A probabilidade de que alguén que non realiza exercicio físico sexa menor de 30 é do 33,33%.

c)

Extraordinaria 2022

Un estudo revela que o 70 % das persoas dunha poboación segue a serie de televisión A, o 60 % segue a serie B e o 30 % solo segue a serie A.

a) Que porcentaxe da poboación segue as dúas series?

b) Se eliximos unha persoa ao chou, cal é a probabilidade de que siga algunha das dúas series?

c) Se eliximos ao chou unha persoa que segue a serie A, cal é a probabilidade de que siga tamén a serie B?

Solución

Sexa \(A\) = {ven a serie A}, \(B\) = {ven a serie B}, segundo o enunciado temos: \(P(A) = 0,7\), \(P(B) = 0,6\) e \(P(A \cap \overline{B}) = 0,3\)

a) Se seguen as dúas series temos o suceso \(A \cap B\).

   Como \(P(A \cap \overline{B}) = P(A - B) = P(A) - P(A \cap B) \implies P(A \cap B) = P(A) - P(A \cap \overline{B}) = 0,7 - 0,3 = 0,4\).

   As persoas que seguen as dúas series é do 40%.

b) Se segue algunha das series temos o suceso \(A \cup B\)

   \(P(A \cup B) = P(A) + P(B) - P(A \cap B) = 0,7 + 0,6 - 0,4 = 0,9\)

   A probabilidade de que alguén sega algunha das series é do 90%.

c) Temos a condición de que segue a serie A, o que pide é \(P(B|A)\).

    \(\displaystyle P(B|A) = \frac{P(A \cap B)}{P(A)} = \frac{0,4}{0,7} = 0,57\)

   A probabilidade de que alguén que segue a serie A, sega tamén a B é do 57%.