... E agora que?

Ordinaria 2025

Debuxe a rexión cerrada pola gráfica de \(\displaystyle f(x) = \sqrt{2x + 1}\), o eixe \(X\) e as rectas \(x = 0\) e \(x = 4\). Logo calcule a súa área.

Solución

A función \(f(x)\) é unha función cun radical o seu dominio é: \(\displaystyle \text{Dom} f = \left[\frac{-1}{2}, +\infty\right)\).  Corta aos eixos nos puntos \((0, 1)\) e \(\displaystyle \left(\frac{-1}{2}, 0\right)\). A área que queremos calcular terá o seguinte aspecto:

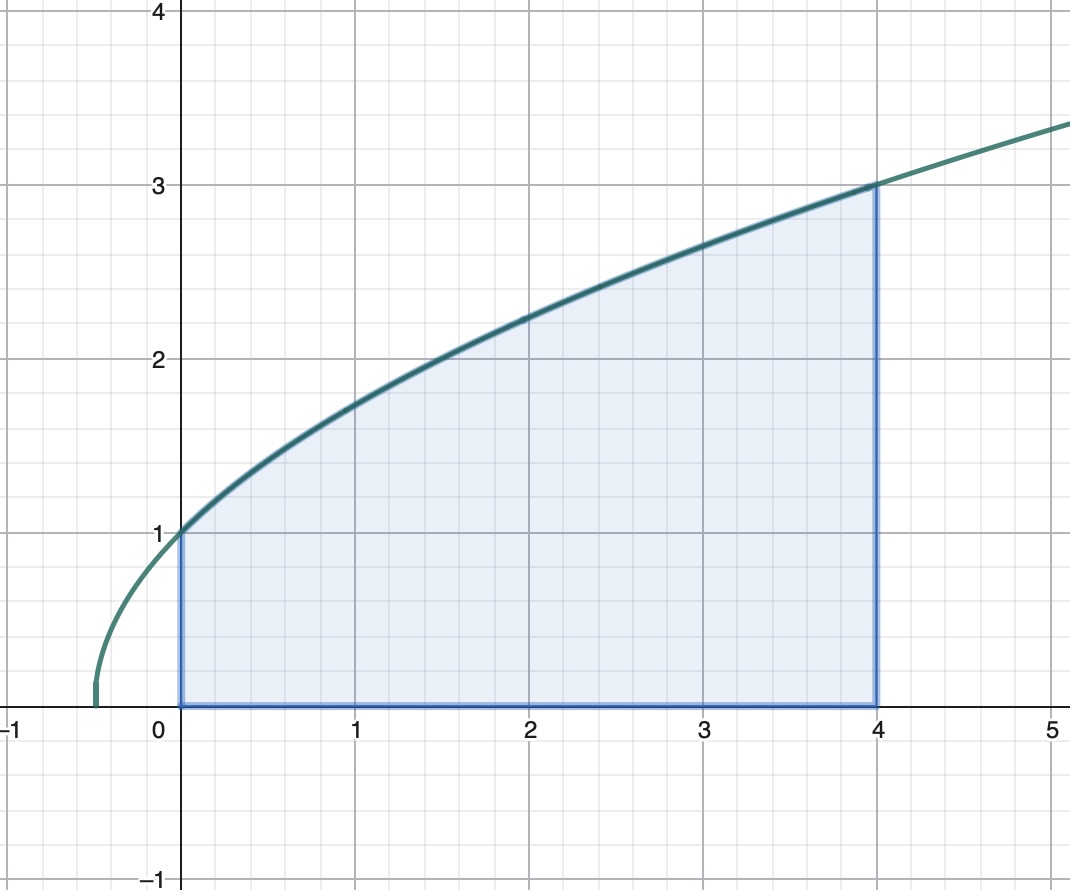
Para calcular a súa área, calculamos a seguinte integral:

\(\displaystyle \int_{0}^4 \sqrt{2x + 1} dx = \frac{1}{2}\int_{0}^4 2\sqrt{2x + 1} dx = \left.\frac{1}{2} \cdot \frac{\sqrt{(2x + 1)^3}}{\frac{3}{2}}\right]_{0}^4 = \left.\frac{\sqrt{(2x + 1)^3}}{3}\right]_{0}^4 = \frac{\sqrt{(2 \cdot 4 + 1)^3}}{3} - \frac{\sqrt{(2 \cdot 0 + 1)^3}}{3} = 9 - \frac{1}{3} = \frac{26}{3} u^2\)

Extraordinaria 2024

Determine o valor do número positivo \(a\) que fai que a área da rexión encerrada pola recta \(y = -2x\) e a parábola \(y = ax^2 + 4x\) sexa igual a 9 unidades cadradas.

Solución

Se \(a\) é positivo a parábola vai ser convexa e vai ter un mínimo en \(\displaystyle f'(x) = 2ax + 4 = 0 \implies x = \frac{-2}{a}\). Os puntos de corte da parábola co eixe X son: \(\displaystyle ax^2 + 4x = 0 \implies x(ax + 4) = 0 \implies x_1 = 0, x_2 = \frac{-4}{a}\)

Os puntos de corte das dúas funcións van ser \(\displaystyle ax^2 + 4x = -2x \implies ax^2 + 6x = 0 \implies x (ax + 6) = 0\), polo que \(x = 0\) e \(\displaystyle x = \frac{-6}{a}\)

Como \(a\) é positiva, tanto o vértice como os puntos de corte calculados, están a esquerda o eixe \(Y\), temos unha situación como a seguinte:

Polo que para calcular a área entre as dúas funcións faremos:

\[\displaystyle \int_{-6/a}^0 \left(-2x - (ax^2 + 4x)\right)dx = \int_{-6/a}^0 \left(-ax^2 - 6x)\right)dx = \left|\left.\frac{-ax^3}{3} - 3x^2\right]_{-6/a}^0\right| = \left|\frac{a(-6/a)^3}{3} + 3(-6/a)^2\right| = \left| \frac{36}{a^2} \right|\]

A fracción que temos vai ser sempre positiva, pois é unha división de números positivos, polo que: \(\displaystyle \left| \frac{36}{a^2} \right| = \frac{36}{a^2} \).

A condición do enunciado é que esa área é 9, logo:

\[\displaystyle \frac{36}{a^2} = 9 \implies a = 2\], xa que \(a\) é un número positivo é a solución \(a = -2\) podemos descartala.