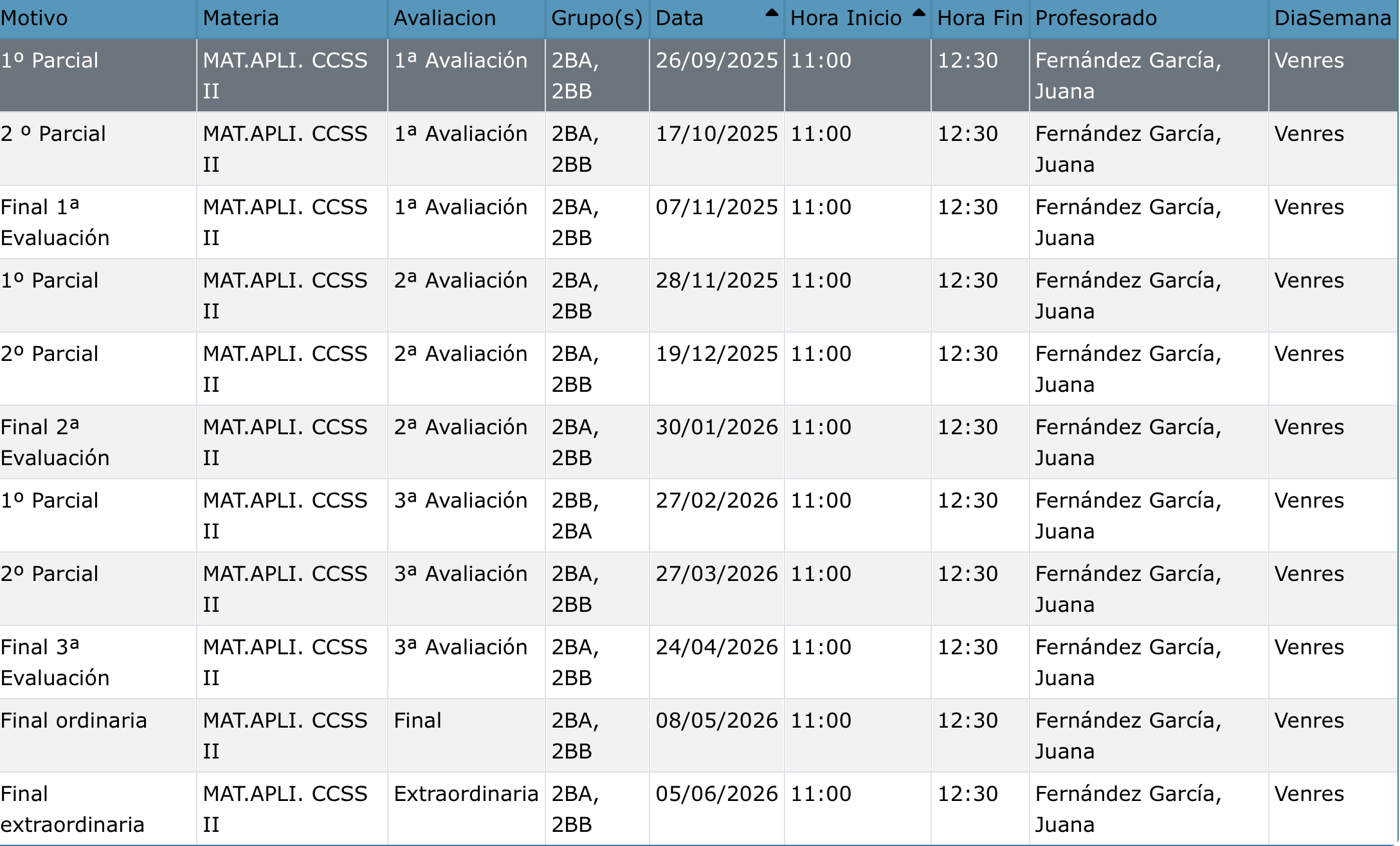
Curso: Matemáticas Aplicadas II - 25/26 | Aula Virtual do IES Fernando Wirtz Suárez
-
Open all
Close all
-
Instructions: Clicking on the section name will show / hide the section.
-
1
Indicaciones generales de este curso
- Toggle -
2
Las clases día a día
- Toggle
La presentación, los apuntes y los ejercicios, los que no se hagan en clase van de deberes para el día siguiente
-
3
Sesiones mes enero 2026
- Toggle-
:Ejercicios selectivad Análisis I contexto económico
-
4
Sesiones mes febrero 2026
- Toggle -
5
-
6
BLOQUE I: ÁLGEBRA
- Toggle
-
- Selectividad España, ejercicios del curso 2025 ordinaria y extraordinaria.
- Ejercicios de los modelos disponibles para el 2026
- Galicia: desde el modelo del 2026 a todas las convocatorias hasta el año 2017
-
7
BLOQUE II: ANÁLISIS MATEMÁTICO
- Toggle
-
This section8
BLOQUE III: PROBABILIDAD Y ESTADÍSTICA
- Toggle -
9
Elabora un modelo de examen aleatorio
- Toggle
- Siguiendo la estructura del último examen realizado por la CIUGA, el examen debería de durar 90´ y constar de 4 preguntas, las dos primeras obligatorias y las dos últimas con opcionalidad A o B.
- Como en nuestro instituto sólo dispondremos de 80’ estará formado por 4 preguntas:
- 3 ejercicios completos PAU o su equivalente en ABAU
- el ejercicio 4 será lo correspondiente a la mitad de otro ejercicio PAU o su equivalente en ABAU.
- Los ejercicios 1 y 2 serán obligatorios y los ejercicios 3 y 4 tendrán opcionalidad entre sus apartados.
- Los ejercicios serán todos seleccionados de forma aleatoria de entre todos los realizados en España desde el 2017 hasta el 2025 incluido el modelo 2026
- Para facilitar la elaboración utilizaremos las siguientes ruletas
-
10
Alumnos pendientes de 1º
- Toggle -
11