REA 08 "E ao final, o Faro!" de Matemáticas de 2º de ESO. cREAgal
Curvas na néboa
Faro de Isla Pancha
Ummm... Parece que la torre de este faro no tiene aristas —observó Uxía extrañada buscando la mirada de don Xulián.
Estás en lo cierto —confirmó el farero—. Este faro, con su base y torre cilíndrica, está diseñado para resistir los embates del viento y las olas del Cantábrico. Su estructura permite que la luz gire uniformemente, alcanzando distancias inimaginables. Pero, ¿sabéis por qué los cilindros son tan importantes para esta función?
Uxía, intrigada, respondió:
—¡Seguro que la clave está en su forma!
Es el momento de explorar los cilindros: sus características, cómo calcular sus áreas y su volumen. Solo así podremos comprender su importancia en los faros.
Lectura facilitada
—Ummm... Parece que la torre de este faro no tiene aristas —dijo Uxía, sorprendida, mirando a don Xulián.
—Tienes razón —confirmó el farero—. Este faro tiene una base y torre cilíndrica, diseñadas para resistir el viento y las olas del Cantábrico. Su forma permite que la luz gire de manera uniforme y llegue muy lejos. Pero, ¿sabéis por qué los cilindros son tan importantes para esta función?
—¡Seguro que la clave está en su forma! —respondió Uxía intrigada.
Ahora es el momento de aprender sobre los cilindros: sus características, cómo calcular sus áreas y su volumen. Solo así entenderemos su papel en los faros.
Cilindro. Definición y elementos
Un cilindro es el cuerpo de revolución que se obtiene al hacer girar un rectángulo alrededor de un eje que pasa por uno de sus lados.
- El lado del rectángulo alrededor del cual gira se llama eje del cilindro.
- Los lados opuestos al eje generan dos círculos, que son las bases del cilindro.
- El lado del rectángulo paralelo al eje da lugar a la superficie lateral del cilindro.
En el siguiente applet puedes observar cómo un rectángulo se transforma en un cilindro recto al girar alrededor de uno de sus lados.
https://www.geogebra.org/m/shevhjaq (Ventana nueva)
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n
Área del cilindro
El área de un cilindro se calcula sumando el área de sus dos bases y de su cara lateral.
Fórmula
Área cilindro = 2 · Área base + Área lateral
- Área base = π r2
- Área lateral = 2 π r h
En el siguiente applet puedes visualizar cómo la superficie lateral del cilindro se "desenrolla" para formar un rectángulo de altura h y anchura igual a la longitud de la circunferencia de la base.
https://www.geogebra.org/m/eefzxcdb (Ventana nueva)
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n
Desafío con cilindros: volúmenes y alturas
Escoge el nivel de dificultad y pon a prueba tus habilidades.
Opción A. Desafío del volumen
Calcula el volumen de los siguientes cilindros ayudándote de los datos que se dan en el applet. Aproxima el resultado a las centésimas.
Cada respuesta correcta suma 2.5 puntos. La puntuación máxima es 10.
https://www.geogebra.org/m/gjsumehn (Ventana nueva)
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n
Opción B. Descubre la altura
Se quiere construir dos cilindros con el mismo volumen. El primero tiene un radio de 3 cm y el segundo un radio de 6 cm.
Ambos cilindros tienen un volumen total de 226 cm³.
- Calcula la altura de cada cilindro.
- ¿Qué relación observas entre el radio y la altura en estos dos cilindros?
Opción C. Ajusta el cilindro
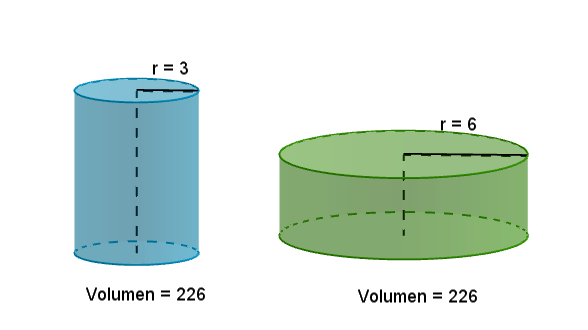
En el siguiente applet hay dos cilindros:
- Cilindro fijo (azul): su volumen es constante.
- Cilindro móvil (verde): puedes modificar su altura desplazando el punto en la vertical.
Cambia la altura del cilindro verde e intenta hacer que su volumen coincida con el del cilindro azul.
https://www.geogebra.org/m/wpftfqhb (Ventana nueva)
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n
Cono de luz
https://www.geogebra.org/m/wbn7swfa (Ventana nueva)
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n
Absorbidos por la lectura del cuaderno de don Xulián, Uxía y su equipo no se dieron cuenta de que la noche había caído. Al levantar la vista, observaron cómo la luz del faro se expandía en la oscuridad con una forma peculiar.
—¡Mirad! —señaló Uxía—. No es solo un haz de luz, parece que se abre en forma de cono.
—Los conos no solo están en la base de muchas estructuras, también determinan cómo se propaga la luz —añadió don Xulián.
Descubramos juntos sus secretos.
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0