REA 08 "E ao final, o Faro!" de Matemáticas de 2º de ESO. cREAgal
Cubicando
Cubicando la Torre de Hércules
https://www.geogebra.org/m/rt59g6wq (Ventana nueva)
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n
Uxía y su equipo observaban planos y cálculos dispersos por la mesa cuando Don Xulián preguntó:
—Antes de construir, ¿cómo calculamos los materiales?
—¿Midiendo? —dudó Uxía.
—Se llama cubicar —explicó el farero que ante las caras de sorpresa prosiguió—. Es decir, hay que calcular dimensiones y materiales según las formas geométricas. De ahí la importancia de analizarlas bien.
Iniciación al volumen
A continuación, se muestran dos prismas formados por 4 cubos unitarios, pero organizados de formas diferentes.
Preguntas:
- ¿Cuál es el área de cada uno de los prismas?
- ¿Y el volumen de cada uno?
Reflexión
A pesar de que los dos prismas tienen una forma diferente, su volumen es el mismo porque ambos están formados por el mismo número de cubos.
Definición
El volumen de un cuerpo es la medida de la cantidad de espacio que ocupa.
Para medirlo, utilizamos unidades cúbicas. La unidad principal es el metro cúbico (m³), que representa el volumen de un cubo de 1 metro de arista.
En general, utilizamos múltiplos y submúltiplos de estas unidades para medir el volumen de objetos más grandes o más pequeños.
Volumen de un ortoedro
En el siguiente applet tienes un ortoedro formado por cubos de 1 unidad cúbica (1 u³).
Instrucciones:
- Ajusta los deslizadores para cambiar el largo, el ancho y la altura del prisma.
- Observa cómo varía el número total de cubos a medida que modificas estas dimensiones.
Preguntas:
- ¿Cómo cambia el volumen cuando aumentas la altura del prisma?
- Si cambias el largo y el ancho del prisma, ¿cómo afecta esto al volumen?
- ¿Cómo puedes calcular el volumen del prisma sin contar los cubos uno a uno?
- ¿Qué relación encuentras entre las dimensiones (largo, ancho, altura) y el volumen del prisma?
https://www.geogebra.org/m/gmjmefvs (Ventana nueva)
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n
Fórmula
Para calcular el volumen de un prisma rectangular, podemos contar cuántos cubos de 1 u³ caben dentro de él.
Si llamamos , y al número de cubos que caben a lo largo, a lo ancho y a lo alto del prisma, el número total de cubos se obtiene multiplicando .
Por lo tanto, la fórmula del volumen de un prisma rectangular recto es:
Donde , y son las dimensiones del prisma (largo, ancho y altura).
Volumen de un prisma
En el siguiente applet se muestran dos representaciones de un prisma:
- El prisma completo, cortado en secciones (rebanadas) horizontales.
- Las mismas rebanadas, desplazadas horizontalmente para formar una figura distinta.
https://www.geogebra.org/m/vhncxtdj (Ventana nueva)
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n
Preguntas:
- ¿Qué puedes decir sobre las rebanadas de las dos figuras? ¿Son iguales en tamaño y forma?
- ¿Tienen las figuras la misma altura total?
- Si las rebanadas tienen el mismo área y altura, ¿el volumen total será el mismo o diferente? ¿Por qué?
- ¿Importa cómo están organizadas las rebanadas para determinar el volumen?
Principio de Cavalieri
Si dos figuras tienen:
- La misma altura.
- Y las secciones paralelas a la base (rebanadas) tienen igual área.
Entonces, los volúmenes de ambas figuras serán iguales, sin importar cómo estén organizadas las secciones ni su forma.
Fórmula del volumen de un prisma
Utilizando el principio de Cavalieri, deducimos la fórmula general para calcular el volumen de un prisma:
Volumen del prisma = Área de la base · Altura del prisma
Practica volumen de ortoedros
Calcula el volumen de los siguientes ortoedros.
Cada respuesta correcta suma 2 puntos y cada fallo resta 1 punto. La puntuación máxima es 10.
https://www.geogebra.org/m/rybymevj (Ventana nueva)
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n
Practica volumen de prismas regulares
Calcula el volumen de los siguientes prismas ayudándote de los datos que se dan en el applet. Aproxima el resultado a las centésimas.
Cada respuesta correcta suma 2.5 puntos. La puntuación máxima es 10.
https://www.geogebra.org/m/ahxt2geu (Ventana nueva)
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n
El volumen de la Torre de Hércules
Imagina que la torre necesita instalar un nuevo sistema de ventilación para mejorar la comodidad de los visitantes y proteger la estructura de la humedad.
Para diseñar este sistema, necesitamos calcular el volumen de dos partes principales de la Torre de Hércules:
- La torre cuadrangular (base del faro).
- La sección octogonal situada debajo de la linterna.
Ignoraremos las escaleras y divisiones internas para simplificar el cálculo.
1. La torre cuadrangular
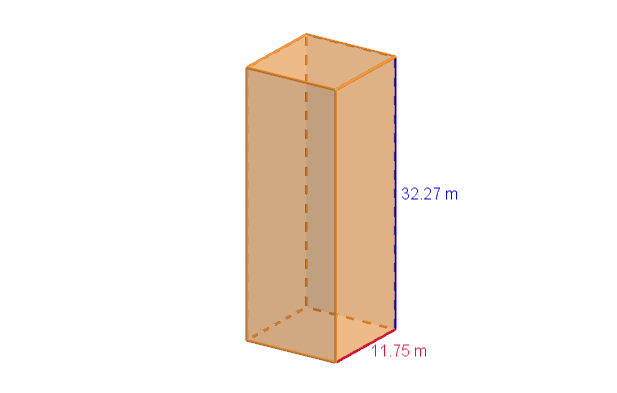
La base del faro es un prisma cuadrangular con las siguientes medidas:
- Lado del cuadrado: 11,75 m.
- Altura del prisma: 32,37 m.
2. La linterna
La sección situada debajo de la lámpara del faro es un prisma octogonal con las siguientes medidas:
- Lado del octógono: 1,9 m.
- Radio del octógono: 2,5 m.
- Altura del prisma: 4,5 m.
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0