Para crear os mapas, elaboraron outro programa en Processing que calculaba as coordenadas proxectadas dos puntos costeiros en diferentes proxeccións cartográficas.
Proxeccións cartográficas utilizadas:
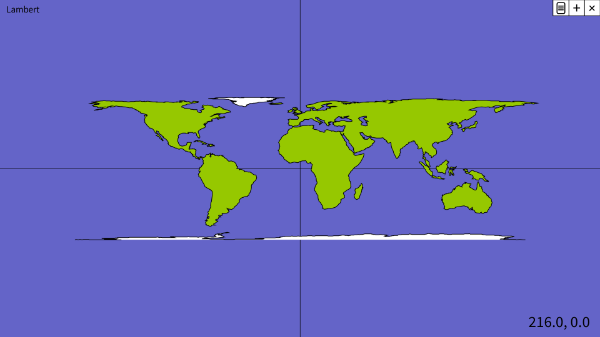
Lambert
Proxección cilíndrica de Lambert (ou de Arquímedes)
- Proxecta horizontalmente os puntos da esfera sobre un cilindro tangente, que se corta por un meridiano e se desenvolve.
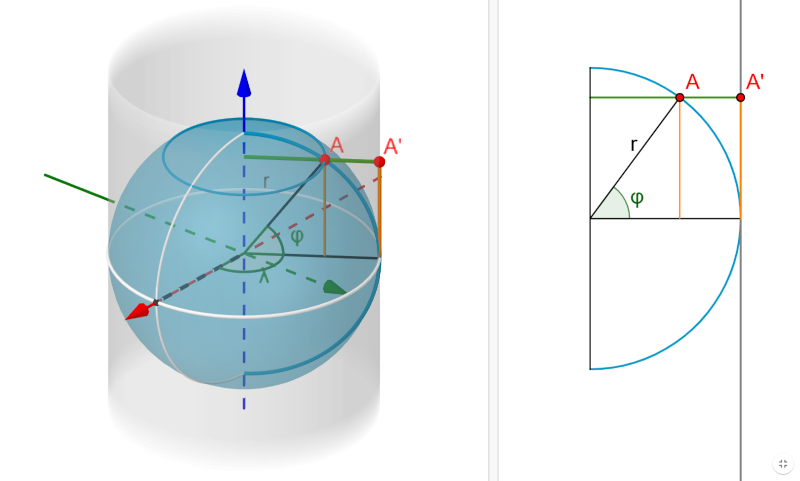
Coordenadas cartesianas dun punto da esfera (λ, φ), en radiáns:
\[
\left \{
\begin{array}{l}
x\;=\;r \; λ \\
y\;=\;r \;sen(φ)
\end{array}
\right .
\]
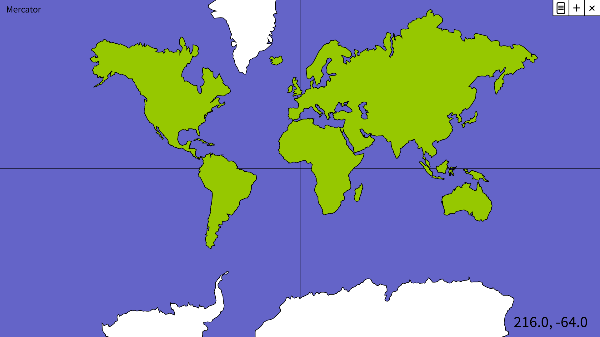
Mercator
- Creada en 1569 por Gerardus Mercator, é unha proxección cilíndrica conforme que conserva os ángulos, o que a fai especialmente útil para a navegación.
- A súa construción orixinal foi empírica e supuxo un avance fundamental na cartografía.
- Máis tarde, co desenvolvemento do cálculo infinitesimal, logrouse a súa formulación matemática exacta.
\[y\;=\;\int \dfrac{1}{cos(φ)} dφ \;=\; ln \left( tan \left( \dfrac{π}{4} +\dfrac{φ}{2} \right) \right)\]
Coordenadas cartesianas dun punto da esfera (λ, φ), en radiáns:
\[
\left \{
\begin{array}{l}
x\;=\; λ \\
y\;=\;ln \left( tan \left( \dfrac{π}{4} +\dfrac{φ}{2} \right) \right)
\end{array}
\right .
\]
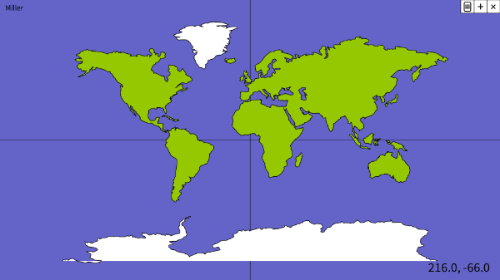
Miller
Modificación de Mercator que comprime a proxección no eixo norte-sur para reducir as distorsións das áreas.
\[
\left \{
\begin{array}{l}
x \; = \; λ \\
y \; = \; \dfrac{5}{4} \; ln \left( tan \left( \dfrac{π}{4} +\dfrac{2 φ}{5} \right) \right)
\end{array}
\right .
\]
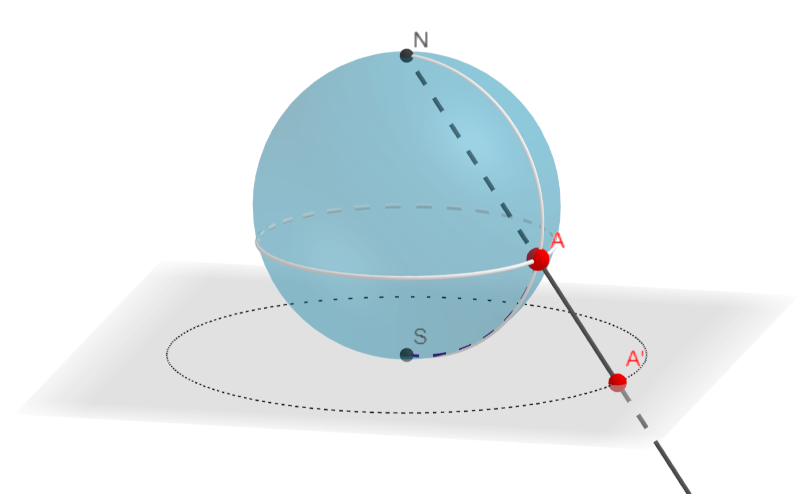
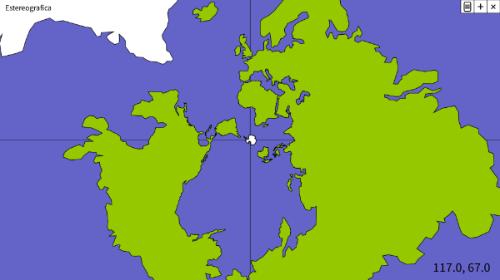
Estereográfica
Atribuída a Hiparco de Nicea, proxecta a esfera desde un punto sobre un plano tangente diametralmente oposto.
\[
\left \{
\begin{array}{l}
x \; =\; 2r \cdot \dfrac{cos(λ) \cdot cos(φ) }{ 1 - sen(φ)} \\
y \; = \; 2r \cdot \dfrac{sen(λ) \cdot cos(φ) }{1 - sen(φ)}
\end{array}
\right .
\]
Código
