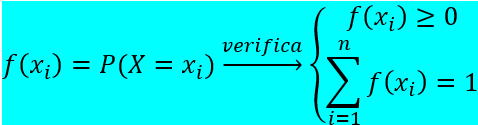DISTRIBUCIONES DISCRETAS

La forma de asignar las probabilidades a cada valor que toma la variable aleatoria, X, se llama distribución de probabilidad.

Una distribución discreta queda determinada si conocemos cualquiera de las siguientes funciones.

La función de probabilidad, f(x), que asigna a cada valor su probabilidad.

función probabilidad discreta

La función de distribución, F(x), que asigna a cada valor la probabilidad de que la variable tome valores menores o iguales que él.

Función de distribución discreta

CÁLCULO DE LA FUNCIÓN DE PROBABILIDAD Y DE LA FUNCIÓN DE DISTRIBUCIÓN DE UNA VARIABLE ALEATORIA DISCRETA

Sea la variable aleatoria X, que cuenta el número de bolas blancas al sacar 2 bolas, sin reemplazamiento, de una urna con 3 bolas blancas y 2 rojas. Calcula sus funciones de probabilidad y de distribución.

PRIMERO. Se determina el espacio muestral y se comprueba que la variable aleatoria definida es discreta.

E={R₁R₂, R₁B₁, R₁B₂, R₁B₃, R₂B₁, R₂B₂, R₂B₃, B₁B₂, B₁B₃, B₂B₃}

Al sacar dos bolas, puede que ninguna sea blanca, que lo sea una o que lo sean las dos. Luego la variable solo toma un número finito de valores. Por tanto, es discreta.

SEGUNDO. Se calculan las probabilidades de los sucesos elementales.

P (X=0) = 1/10=0.1	P (X=1) = 6/10=0.6	P (X=2) = 3/10=0.3
P (X≤0) =0.1	P (X≤1) =0.7	P (X≤2) =1

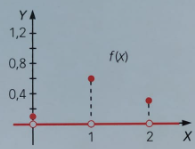
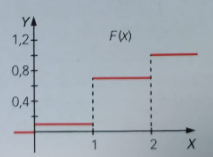
TERCERO. Se escriben las funciones de probabilidad, f(x), y de distribución, F(x), y se representan.

f(x)=\left\lbrace\begin{array}{ll} 0.1 &\mbox{si }x=0\\ 0.6 &\mbox{si }x=1\\0.3 &\mbox{si }x=2\\0&\mbox{en el resto de valores}\end{array}\right. \hspace{1cm} F(x)=\left\lbrace\begin{array}{ll} 0 &\mbox{si }-\infty <x<0\\ 0.1 &\mbox{si }0\leq x<1\\0.7 &\mbox{si }1\leq x<2\\1&\mbox{si }2\leq x<+\infty\end{array}\right.