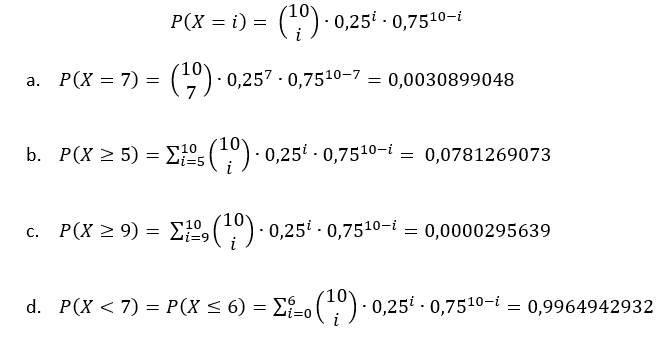Hay numerosas situaciones de la vida cotidiana que se resuelven mediante una distribución binomial, B(n, p).
Veamos un ejemplo de cómo calcular probabilidades en variables aleatorias que siguen una distribución binomial:
Un examen tipo test consta de 10 preguntas, cada una de las cuales tiene cuatro posibles respuestas de las que solo una es correcta. Si contestamos al azar, calcula las siguientes probabilidades.
- Acertar siete respuestas.
- Aprobar el examen.
- Tener sobresaliente.
- No llegar al notable.
PRIMERO. Se define la variable aleatoria discreta que se utilizará.
X= <<Número de aciertos en el examen>>
SEGUNDO. Se calculan los parámetros de la distribución.
n → número de veces que se realiza el experimento, es decir, las preguntas que se contestan al azar, 10 → n = 10
p → probabilidad de obtener un acierto cuando se contesta al azar → p = P(<<Acertar la pregunta>>)=1/4=0,25
Se tiene entonces que X ≡ B(10; 0,25)
TERCERO. Se escribe cada uno de los sucesos en función de los valores de la variable aleatoria.
- Acertar 7 respuestas → X = 7
- Aprobar el examen → X ≥ 5
- Tener sobresaliente → X ≥ 9
- No llegar al notable → X < 7
CUARTO. Se calculan las probabilidades pedidas con ayuda de la función de probabilidad.