La carrera (Tarea LEMA)
Tarea
La profesora de Educación Física ha preparado una nueva prueba de velocidad que consiste en lo siguiente:
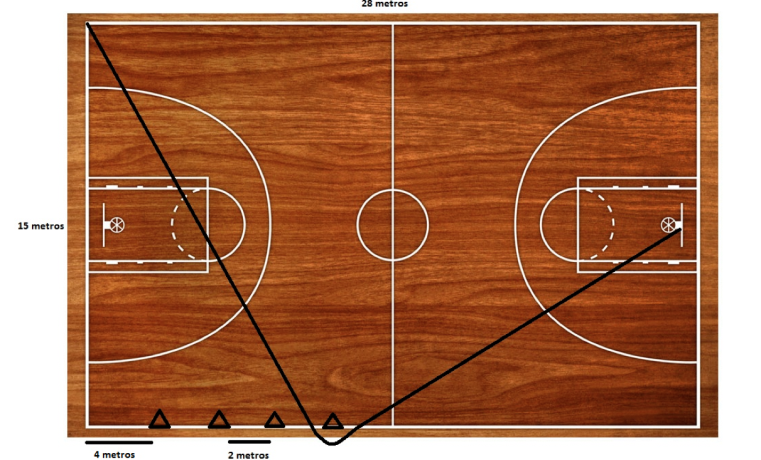
- Coloca 10 conos a lo largo de la línea lateral de la cancha de baloncesto, empezando a 4 metros de la línea de fondo y separados entre sí 2 metros.
- Cada corredor sale desde la esquina opuesta, rodea el cono que quiera y corre hasta tocar la canasta del otro lado.
¿Tiene alguna importancia el cono que decidamos rodear en la carrera? ¿Qué haríais vosotros para intentar ganarla? Si pudierais añadir un nuevo cono, ¿dónde lo pondríais?
Ayuda
Enlace a la actividad GeoGebra: https://www.geogebra.org/m/kstvcw8g
Una posible solución
Para determinar el cono que debemos rodear para que la distancia sea mínima podemos calcularlas todas utilizando una hoja de cálculo (de GeoGebra o Calc)
- En la primera fila introducimos las etiquetas y en la siguiente las fórmulas
| A | B | C | D | E | F | |
| 1 | Nº de conos | cateto del 1º triángulo |
hipotenusa del 1º triángulo) |
cateto del 2º triángulo | hipotenusa del 2º triángulo | distancia recorrida |
| 2 | 1 | 4 | = sqrt(15^2 + B2^2) | = 28 - B2 | = sqrt(7.5^2 + D2^2) | = C2 + E2 |
| 3 | =A2+1 | = B2 + 2 |
- Arrastramos las fórmulas hacia abajo.
Para calcular la distancia a la que pondríamos un nuevo cono:
- Definimos la función \( d(x) = \sqrt{15^2 +x^2} \;+ \;\sqrt{7.5^2 +(28-x)^2} \;\)
- Con la herramienta "Extremos relativos" obtenemos el mínimo de la función.
Solución en GeoGebra
Mediante una hoja de cálculo (de GeoGebra o Calc)
Enlace a la actividad en GeoGebra: https://www.geogebra.org/m/e3nfj87a