Section outline
-
-
Students mustMarcar como feito
-
-
Proxecto consistente na xeración de moldes das dovelas dun arco e a súa reproducción en mortero, cemento, escaiola, etc.
O deseño dos moldes faráse usando os programas gratuitos:
- GeoGebra.
- Inkscape.
- Tinkercad
A partires dos deseños dos moldes, xeraránse os arquivos STL deses deseños e se imprimirán nunha impresora 3D. O molde impreso usaráse para xerar as pezas (dovelas) do arco e construir o arco.
Partes dun arco:
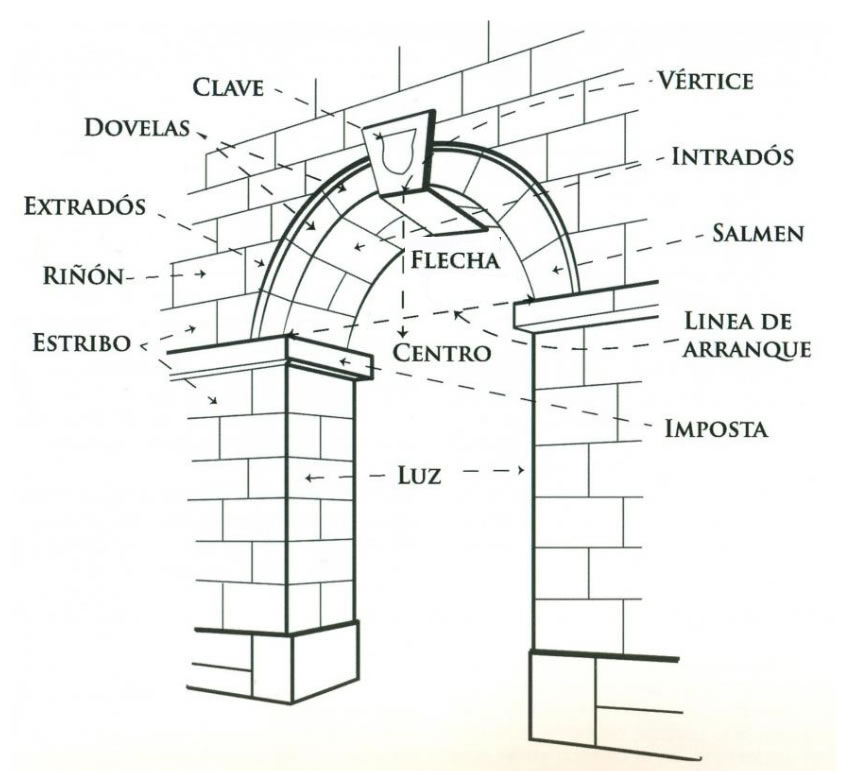
Tipos de arco:
Fuente: Diccionario visual de Términos arquitectónicos. Ed. Cátedra
-
Students mustMarcar como feito
Guía para xerar o encofrado (o molde para as pezas) para reproducir un arco usando GeoGebra.
(Documento modificado a comezos do mes de marzo)
-
Students mustMarcar como feito
Guía para xerar o arquivo de impresión 3D do encofrado (o molde para as pezas) para reproducir un arco.
(A partir do deseño realizado en GeoGebra e usando Inkscape e Tinkercad para obter o arquivo stl de impresión 3D).
(Documento modificado a comezos do mes de marzo)
-
Students mustMarcar como feito
Parte dun documento publicado pola Región de Murcia sobre a construcción xeométrica de arcos.
Lembra que, nas partes onde o arco se constrúe usando arcos de circunferencia, o centro do arco da cincunferencia interior e exterior debe selo mesmo.
Título: Geometría de los arcos. Guía para la construcción y trazado de arcos
-
Students mustMarcar como feito
Envía:
- Un documento de texto onde figure o nome ou nomes dos autores e o ancho e alto de cada unha das pezas do molde para facelo arco.
- Os arquivos GeoGebra das pezas do molde do arco.
- Os arquivos Inskscape das pezas do molde do arco.
- Os arquivos stl das pezas do molde do arco.
Cando teñas subido todos eses arquivosa, avisa o profesor ou profesora responsable desta actividade (para que saiba que subiches or arquivos dun arco para imprimir).
-
-
Teselados nazaríes y de Escher (lagarto nº 25)
Un teselado consiste en realizar un recubrimiento del plano usando una o varias figuras geométricas (teselas).
Se puede hacer un teselado usando figuras geométricas simples como, por ejemplo, un triángulo equilátero, un cuadrado, un rectángulo o un hexágono regular.
Pero hay muchas más formas que permiten hacer un teselado. Algunas muy complejas geométricamente. A veces solo se usa una figura geométrica pero otras veces se usan dos figuras distintas o incluso tres.
Entre los teselados más famosos se encuentran los teselados de la Alhambra de Granada. Esos teselados sirvieron de inspiración al artista neerlandés M.C. Escher para hacer parte de sus obras.
La creación de teselas que dan lugar a un teselado del plano se considera una de las formas en la que se observa la vinculación de las Matemáticas con el mundo del Arte.
-
Students mustMarcar como feito
Información sobre teselados y las condiciones que debe cumplir una figura geométrica o tesela para recubrir adecuadamente el plano.
-
Students mustMarcar como feito
Información sobre teselados y las condiciones que debe cumplir una figura geométrica o tesela para recubrir adecuadamente el plano.
-
Students mustMarcar como feito
Información sobre teselados y las condiciones que debe cumplir una figura geométrica o tesela para recubrir adecuadamente el plano.
-
Students mustMarcar como feito
Creación de un cortador de teselas de arcilla o arcilla polimérica: 1ª parte
Guía de generación de tesela: proceso de generación de la figura geométrica.
- Uso de GeoGebra
- Uso del recurso tiled.art
El cortador podría servir también para cortar materiales diferentes de la arcilla. Solo habría que imprimir el cortador usando el material adecuado.
-
Students mustMarcar como feito
Guía de creación de un cortador de teselas de arcilla o arcilla polimérica: 2ª parte
- Modificación en Inkscape del archivo svg generado previamente en GeoGebra o tiled.art.
- Generación del archivo stl de impresión 3d del cortador.
El cortador podría servir también para cortar materiales diferentes de la arcilla. Solo habría que imprimir el cortador usando el material adecuado.
-
Students mustMarcar como feito
Ejemplos de cortadores y de piezas cortadas.
Los cortadores se crearon en el Instituto imprimiendo diseños propios en la impresora 3D de polos creativos (salvo el diseño 2D del lagarto de Escher).
El diseño 2D del lagarto de Escher utilizado es un archivo svg de dominio público. El autor de ese diseño es Sean Michael Ragan (https://www.seanmichaelragan.com/html/%5B2008-04-18%5D_MC_Escher_lizard_vector_art.shtml)
-
-
Un teselado periódico es un teselado que presenta un patrón que se repite. Los teselados más antiguos son teselados periódicos.
Por ejemplo, las teselas en forma de triángulos, rectángulos, hexágonos y las teselas nazaríes de la Alhambra dan lugar a teselados periódicos.
Teselado. Tesela con forma de hexágono regular
La existencia de teselados periódicos dio lugar hace ya tiempo a que los matemáticos se planteasen una pregunta: ¿existen teselados no periódicos? Es decir, ¿existen teselas que den lugar a un teselado en el que no exista un patrón que se repita? A ese tipo de teselados se los denominó como teselados aperiódicos.
Con el paso del tiempo fueron surgiendo teselados aperiódicos pero formados por varias figuras geométricas. En los años 70 el matemático Roger Penrose descubrió un teselado aperiódico formado a partir de 6 figuras geométricas diferentes. A ese teselado se le denominó teselado P1.
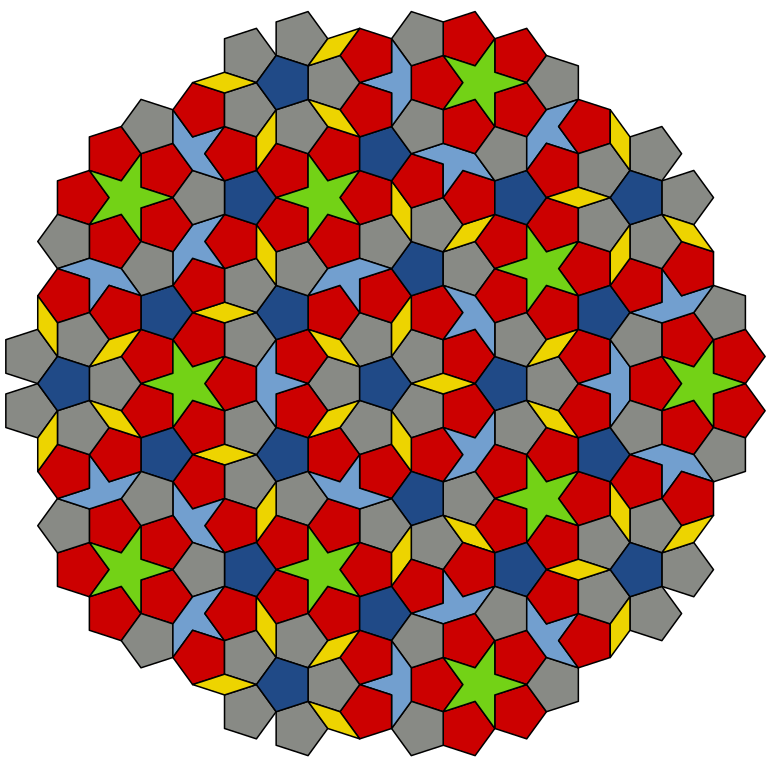
Teselado de Penrose P1
Fuente: Viquipedia
Unos años más tarde descubrió dos teselados aperiódicos diferentes, formados por dos teselas cada uno de ellos. Son los teselados de Penrose, denominados como P2 (formado por dos cuadriláteros denominados "cometa" y "flecha") y P3 (formado por dos rombos).
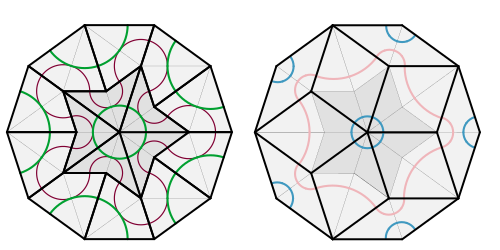
Teselado de Penrose P2 y P3.
Fuente: WikimediaArtículo de la Gaceta de la RSME sobre teselados de Penrose: https://gaceta.rsme.es/abrir.php?id=35
Después del descubrimiento de Penrose surgió una nueva pregunta: ¿existe un teselado aperiódico formado a partir de una única tesela? Ese problema matemático se llamó problema de "einstein" (de "ein stein", palabras alemanas que significan "una piedra").
En el año 2022, el matemático amateur David Smith pensó que había encontrado una solución al problema con una tesela con forma de un polígono de 13 lados que se denominó "hat". En 2023 los matemáticos Craig S. Kaplan, Joseph Samuel Myers y Chaim Goodman-Strauss demostraron que la tesela "hat" generaba un teselado aperiódico y encontraron dos teselas más que generan un teselado aperiódico. A esas teselas se las denominó "turtle" y "spectre".
Tesela "Hat"
Fuente: University of Cambridge
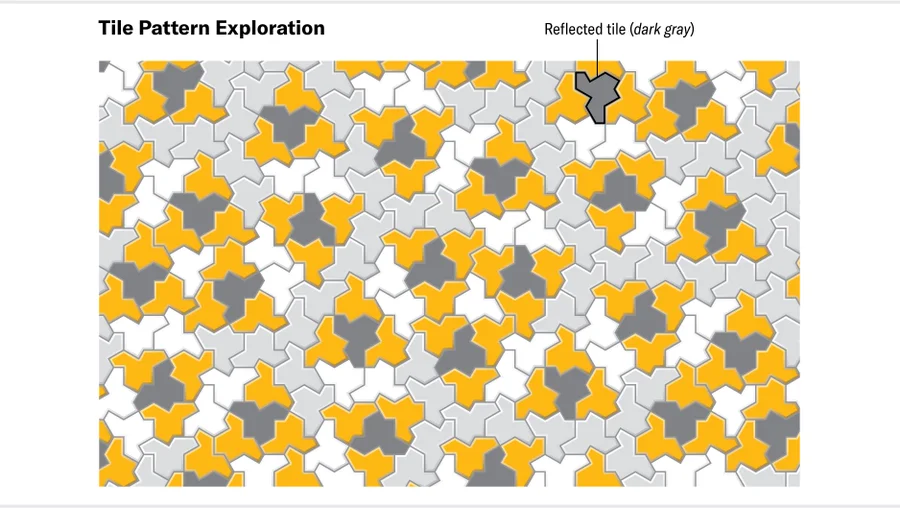
Teselación usando la tesela "Hat"
Fuente: Scientific American
Teselado usando la tesela "Turtle"
Fuente: Etsy
Puzzle basado en la tesela "Spectre"
Fuente: Nervous SystemLos teselados aperiódcos están relacionados con los cuasicristales (formas estructurales ordenadas pero no periódicas) estudiados por el premio Nobel de Química Dan Shechtman.
En realidad las teselas "hat", "turtle" y "spectre" forman parte de una "familia" de teselas que generan un teselado aperiódico. Los siguientes enlaces sirven para generar ese tipo de teselas. Las teselas generadas en esos recursos pueden exportarse en formato png y svg (consulta el documento "Generación de teselas: Parte 2" del apartado anterior para saber cómo generar un cortador de arcilla a partir de un gráfico en formato svg).
https://somethingorotherwhatever.com/aperiodic-monotile/interactive.html
https://cs.uwaterloo.ca/~csk/hat/h7h8.html
Más información sobre el "problema de einstein":
Aunque surgieron como un problema matemático, los teselados aperiódcos son importantes en otras disciplinas. Por ejemplo, están relacionados con los cuasicristales (formas estructurales ordenadas pero no periódicas) estudiados por el Premio Nobel de Química Dan Shechtman.
-
Guía que explica el proceso que se puede seguir para generar un sello a partir de una imagen.
A partir de la imagen, se generará un diseño 3D que se imprimirá en una impresora 3D.
Una vez impreso el sello, se puede utilizar con arcilla pero también se puede utilizar con otros materiales (jabón, lacre, cuero,...).
