Teselados aperiódicos

Un teselado periódico es un teselado que presenta un patrón que se repite. Los teselados más antiguos son teselados periódicos.

Por ejemplo, las teselas en forma de triángulos, rectángulos, hexágonos y las teselas nazaríes de la Alhambra dan lugar a teselados periódicos.

Teselado. Tesela con forma de hexágono regular

La existencia de teselados periódicos dio lugar hace ya tiempo a que los matemáticos  se planteasen una pregunta: ¿existen teselados no periódicos? Es decir, ¿existen teselas que den lugar a un teselado en el que no exista un patrón que se repita? A ese tipo de teselados se los denominó como teselados aperiódicos.

Con el paso del tiempo fueron surgiendo teselados aperiódicos pero formados por varias figuras geométricas. En los años 70 el matemático Roger Penrose descubrió un teselado aperiódico formado a partir de 6 figuras geométricas diferentes. A ese teselado se le denominó teselado P1.

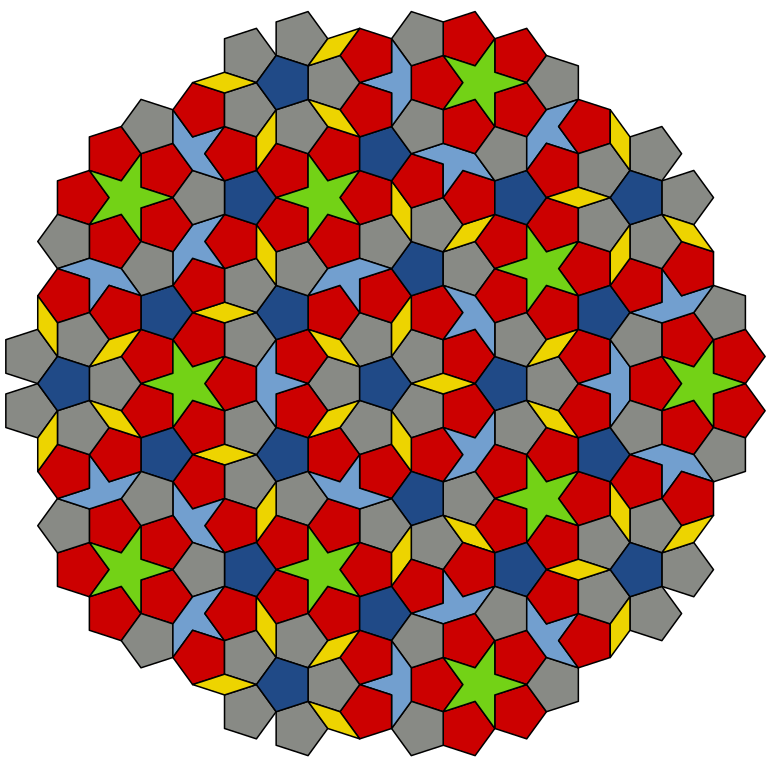
Teselado de Penrose P1

Fuente: Viquipedia

Unos años más tarde descubrió dos teselados aperiódicos diferentes, formados por dos teselas cada uno de ellos. Son los teselados de Penrose, denominados como P2 (formado por dos cuadriláteros denominados "cometa" y "flecha") y P3 (formado por dos rombos).

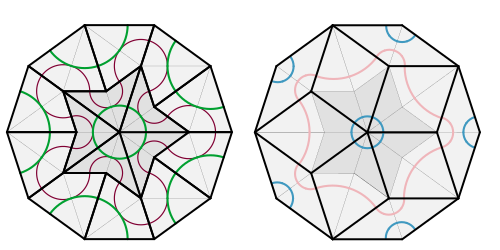
Teselado de Penrose P2 y P3.
Fuente: Wikimedia

Artículo de la Gaceta de la RSME sobre teselados de Penrose: https://gaceta.rsme.es/abrir.php?id=35

Después del descubrimiento de Penrose surgió una nueva pregunta: ¿existe un teselado aperiódico formado a partir de una única tesela? Ese problema matemático se llamó problema de "einstein" (de "ein stein", palabras alemanas que significan "una piedra").

En el año 2022, el matemático amateur David Smith pensó que había encontrado una solución al problema con una tesela con forma de un polígono de 13 lados que se denominó "hat".  En 2023 los matemáticos Craig S. Kaplan, Joseph Samuel Myers y Chaim Goodman-Strauss demostraron que la tesela "hat" generaba un teselado aperiódico y encontraron dos teselas más que generan un teselado aperiódico. A esas teselas se las denominó "turtle" y "spectre".

Tesela "Hat"

Fuente: University of Cambridge

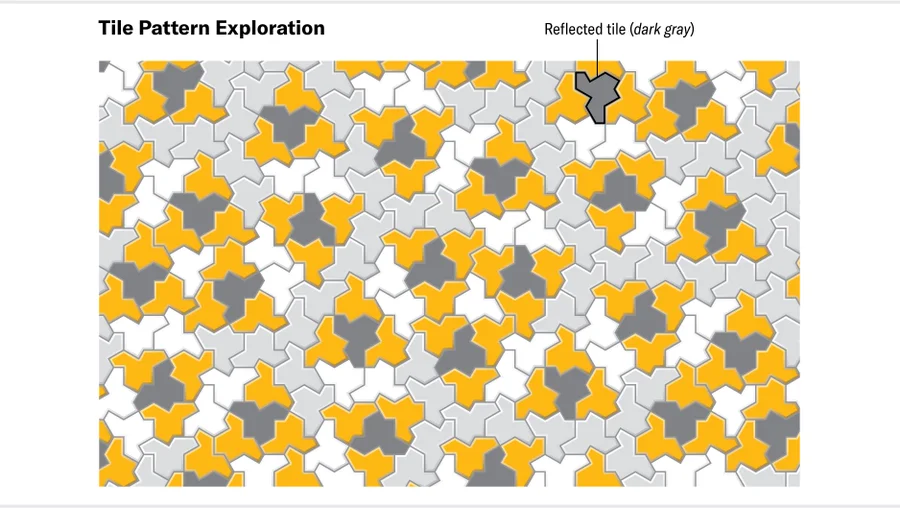
Teselación usando la tesela "Hat"
Fuente: Scientific American

Teselado usando la tesela "Turtle"
Fuente: Etsy

Puzzle basado en la tesela "Spectre"
Fuente: Nervous System

Los teselados aperiódcos están relacionados con los cuasicristales (formas estructurales ordenadas pero no periódicas) estudiados por el premio Nobel de Química Dan Shechtman.

En realidad las teselas "hat", "turtle" y "spectre" forman parte de una "familia" de teselas que generan un teselado aperiódico. Los siguientes enlaces sirven para generar ese tipo de teselas. Las teselas generadas en esos recursos pueden exportarse en formato png y svg (consulta el documento "Generación de teselas: Parte 2" del apartado anterior para saber cómo generar un cortador de arcilla a partir de un gráfico en formato svg).

https://somethingorotherwhatever.com/aperiodic-monotile/interactive.html

https://cs.uwaterloo.ca/~csk/hat/h7h8.html

Más información sobre el "problema de einstein":

https://www.scientificamerican.com/article/inside-mathematicians-search-for-the-mysterious-einstein-tile/

Aunque surgieron como un problema matemático, los teselados aperiódcos  son importantes en otras disciplinas. Por ejemplo, están relacionados con los cuasicristales (formas estructurales ordenadas pero no periódicas) estudiados por el Premio Nobel de Química Dan Shechtman.