Filtros Pasivos
FILTROS PASIVOS
Os filtros son circuítos electrónicos que se empregan para bloquear certas frecuencias dun sinal. Construense a partir de resistencias, bobinas e condensadores e basean o seu funcionamento na variabilidade da reactancia ca frecuencia.
Aqueles filtros que permiten o paso de baixas frecuencias e bloquean as altas frecuencias chámanse filtros de paso baixo ou filtros pasa baixas.
Si permiten o paso de altas frecuencias e bloquean as baixas frecuencias chámanse filtros de paso alto ou filtros pasa altas.
Si só permiten o paso dunha banda de frecuencia bloqueando as baixas e as altas chámanse filtros pasa banda.
Si, polo contrario bloquean unha banda de frecuencias e permiten o paso de todo o resto do espectro chámanse filtros de banda eliminada.

Nesta unidade centraremonos en filtros pasivos, que son aqueles compostos exclusivamente por resistencias, bobinas e/ou condensadores sen que interveña no circuíto ningún elemento activo tal como amplificadores operacionales. Os filtros activos abordaranse no segundo trimestre.
Filtros de primeiro orden
Son aqueles formados por unha resistencia e un só elemento reactivo (un condensador ou unha bobina). Veremos primeiro os filtros RC e despois os RL.
Filtro RC Pasa Baixas
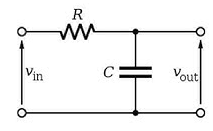
Recorda: \[X_c = \frac{1}{\omega · C} = \frac{1}{2 · \pi · f · C}\]
Para frecuencias baixas o condensador compórtase coma un circuíto aberto (reactancia infinita). Polo tanto o sinal de entrada aparece á saída sen atenuación ( Ganancia =1 ou equivalentemente Ganancia = 0 dB)
Para frecuencias altas o condensador compórtase coma un curtocircuíto (reactancia cero). Polo tanto a saída estará conectada a terra ( 0 V).
Precisamos entón calcular a qué frecuencia intermedia o circuíto cambia de comportamento. Por convenio, considérase a frecuencia de corte aquela frecuencia á que se igualan R e Xc
\[R=X_c → R = \frac{1}{2\pi f_c C} →f_c=\frac{1}{2\pi R C} \]
Nesta situación a tensión de saída virá dada polo divisor:
\[V_{out} = V_{in} \frac{X_c}{Z}=V_{in} \frac{R}{\sqrt{R^2 + {X_c}^2}}=V_{in} \frac{R}{\sqrt{R^2 + R^2}}=V_{in} \frac{R}{\sqrt{2R^2}}=V_{in} \frac{R}{R\sqrt{2}}=V_{in} \frac{1}{\sqrt{2}} =0,7 V_{in} \]
Polo tanto á frecuencia de corte, a ganancia do filtro é: \[ G=\frac{V_{out}}{V_{in}}=0,7 → G = 20 log 0,7 = -3 dB\]
A frecuencia de corte dun filtro de 1º orde é aquela á que a ganancia é de -3dB, o que equivale ó 70% do sinal orixinal.
Observa o diagrama de Bode (ganancia - frecuencia) dun filtro pasa baixa de exemplo:
Se non sabes qué é un DIAGRAMA DE BODE, PINCHA AQUÍ.

A frecuencias baixas a ganancia é plana e igual a 0dB. A 159 Hz presenta unha ganancia de -3dB. Esa é a frecuencia de corte. A partir deste punto a ganancia vai a caer a un ritmo de -20 dB por década. (Unha década é o tramo na que a frecuencia se multiplica por 10)
O ancho de banda do filtro BW (BandWidth) = 159 Hz
EXERCICIO 1:
Simular en LTspice o seguinte filtro.

Configurar a fonte da seguinte maneira:

E o análisis de frecuencia:
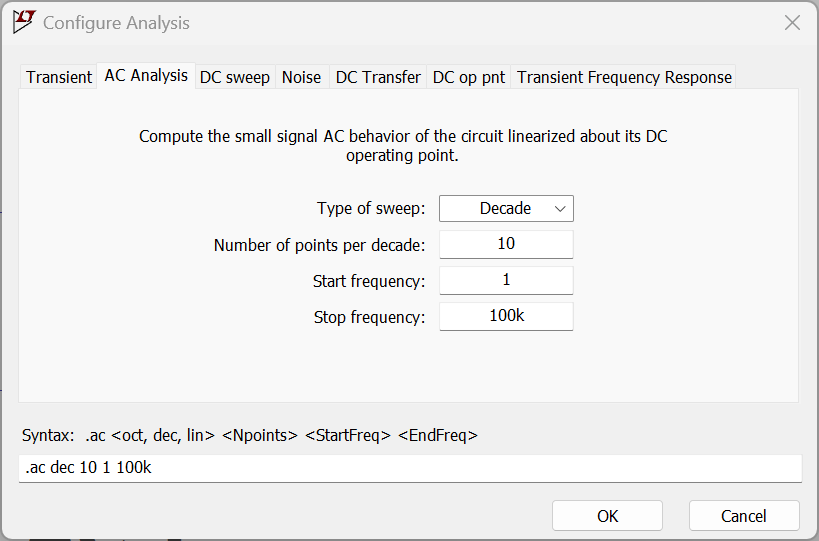
Entregar no documento:
- A frecuencia de corte calculada e a obtida gráficamente.
- Captura do diagrama de Bode. (Só nos interesa a magnitude, non a fase.)
- Estimar a atenuación na banda eliminada. ( O valor teórico é de -20 dB/Dec , pero ides obter un valor diferente.)
Filtro RC Pasa Altas
Intercambiando a resistencia e o condensador temos un filtro pasa altas.
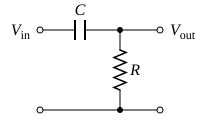
A expresión da frecuencia de corte é a misma que no filtro anterior:
\[f_c=\frac{1}{2\pi R C} \]
E o diagrama de Bode presenta este aspecto:
EXERCICIO 2: Simular en LTspice o seguinte filtro.
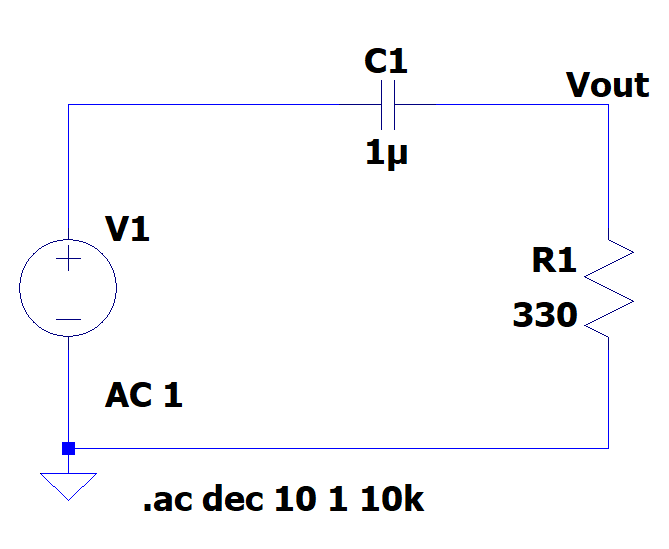
Entregar no documento:
- A frecuencia de corte calculada e a obtida gráficamente.
- Captura do diagrama de Bode. (Só nos interesa a magnitude, non a fase.)
- Estimar a atenuación na banda eliminada. ( O valor teórico é de -20 dB/Dec , pero ides obter un valor diferente.)
Filtro RC Pasa Banda
Combinando un filtro pasa baixas e un pasa altas podemos obter un filtro pasa banda. Este tipo de filtros ten dúas frecuencias de corte: a inferior e a superior.
EXERCICIO 3: Simular en LTspice o seguinte filtro.

Ó simular este filtro, observarás que a banda pasante ten unha ganancia de -2,3 dB. Polo tanto, as dúas frecuencias de corte estarán en -5,3 dB.
Entregar no documento:
- As frecuencias de corte calculadas e as obtidas gráficamente.
- Captura do diagrama de Bode. (Só nos interesa a magnitude, non a fase.)
- Estimar a atenuación na banda eliminada. ( O valor teórico é de -20 dB/Dec , pero ides obter un valor diferente.)
O filtro de banda eliminada é máis complexo. Deixámolo para cando vexamos filtros activos.
Filtro RL Pasa Baixas
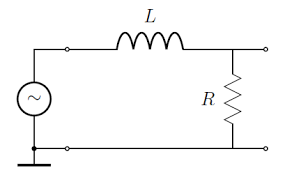
A frecuencias baixas XL e casi 0 , polo que Vout=Vin. A frecuencias altas, XL faise alta, polo que Vout faise cada vez máis pequeno.
A frecuencia de corte é aquela á que R = XL :
\[ R=L \omega _c → R = 2 \pi f_c L → f_c = \frac{R}{2 \pi L}\]
EXERCICIO 4: Simular en LTspice o seguinte filtro. Trátase do filtro dun subwoofer. Si non sabes o qué é un subwoofer xa tardas en buscalo. Investiga tamén qué é un crossover de audio.
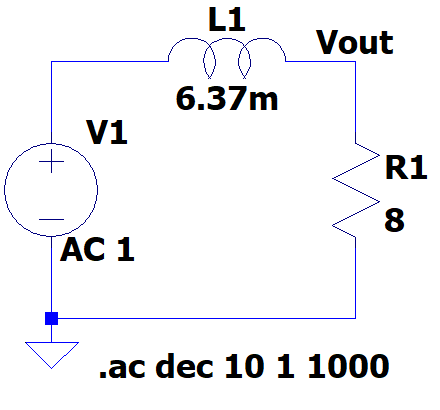
Entregar no documento:
- A frecuencia de corte calculada e a obtida gráficamente.
- Captura do diagrama de Bode. (Só nos interesa a magnitude, non a fase.)
Filtro RL Pasa Altas
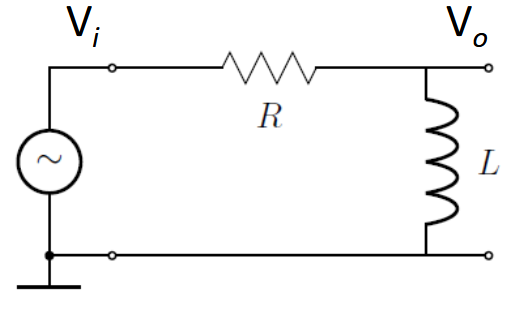
A frecuencia de corte calcúlase mediante a mesma expresión que no caso anterior: \[ f_c = \frac{R}{2 \pi L}\]
EXERCICIO 5: Deseñar e simular un filtro RL pasa altas para un tweeter con fc=2 kHz e L=47 mH.
Entregar no documento:
- Cálculo de R.
- A captura do esquema do circuíto.
- Captura do diagrama de Bode. (Só nos interesa a magnitude, non a fase.)
