Repaso de conceptos previos

Definición de función real de variable real

Expresiones de una función

• Expresión algebraica. Es la relación matemática entre las dos variables en la que la variable dependiente ( y ) está despejada. No siempre es posible obtener la expresión analítica de una función. La expresión analítica suele utilizarse en física, química, economía, etc.
• Tabla de valores. Es un conjunto de pares de valores (x,y) de la función.
  
• Gráfica. La gráfica es el conjunto de todos los puntos (x,y=f(x)) representados en los ejes de coordenadas cartesianos,.
  

Ejemplo:

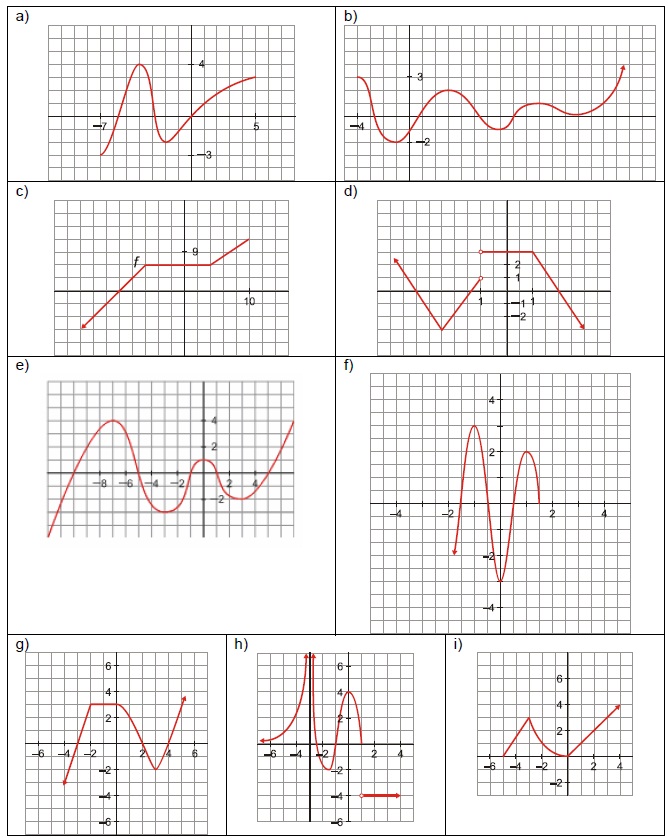
Cómo distinguir una función

Características de una función

1. Dominio y recorrido

2. Continuidad

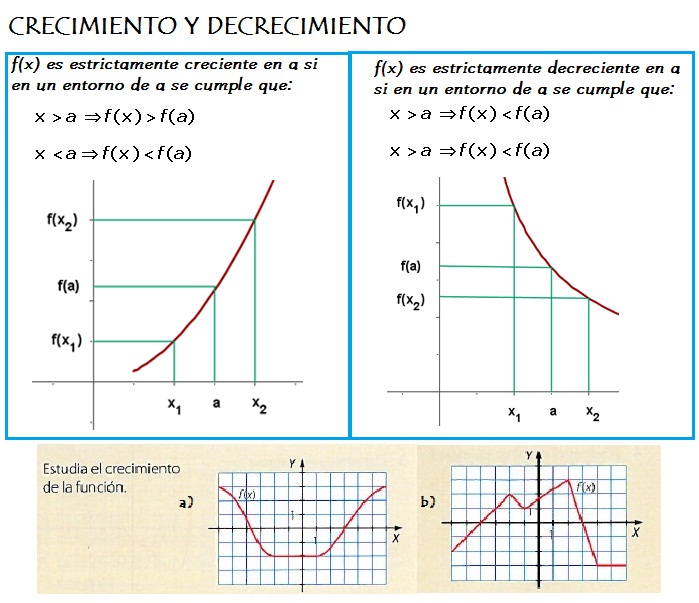
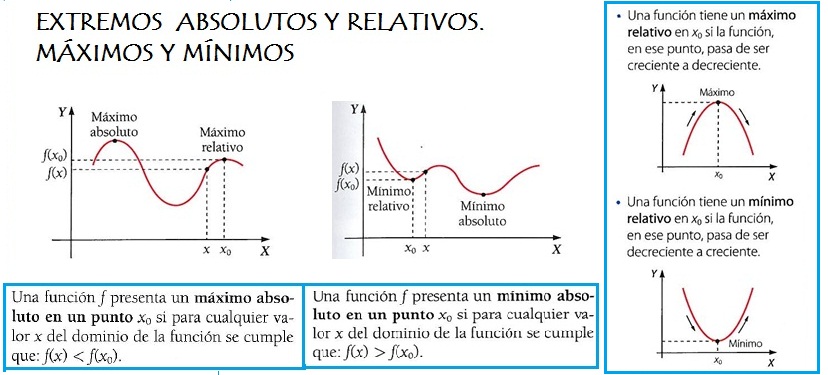
3. Monotonía: crecimiento y decrecimiento; máximos y mínimos.

4. Curvatura: concavidad, convexidad y punto de inflexión.

Diremos que una función es CÓNCAVA o presenta su concavidad hacia abajo cuando dados dos puntos cualesquiera el segmento que los une queda por debajo de la curva.
Análogamente, diremos que es CONVEXA o presenta su concavidad hacia arriba si dados dos puntos de la curva el segmento que los une queda por encima de la curva.
Los puntos en los que la curvatura pasa de cóncava a convexa o viceversa se llaman PUNTOS DE INFLEXIÓN.

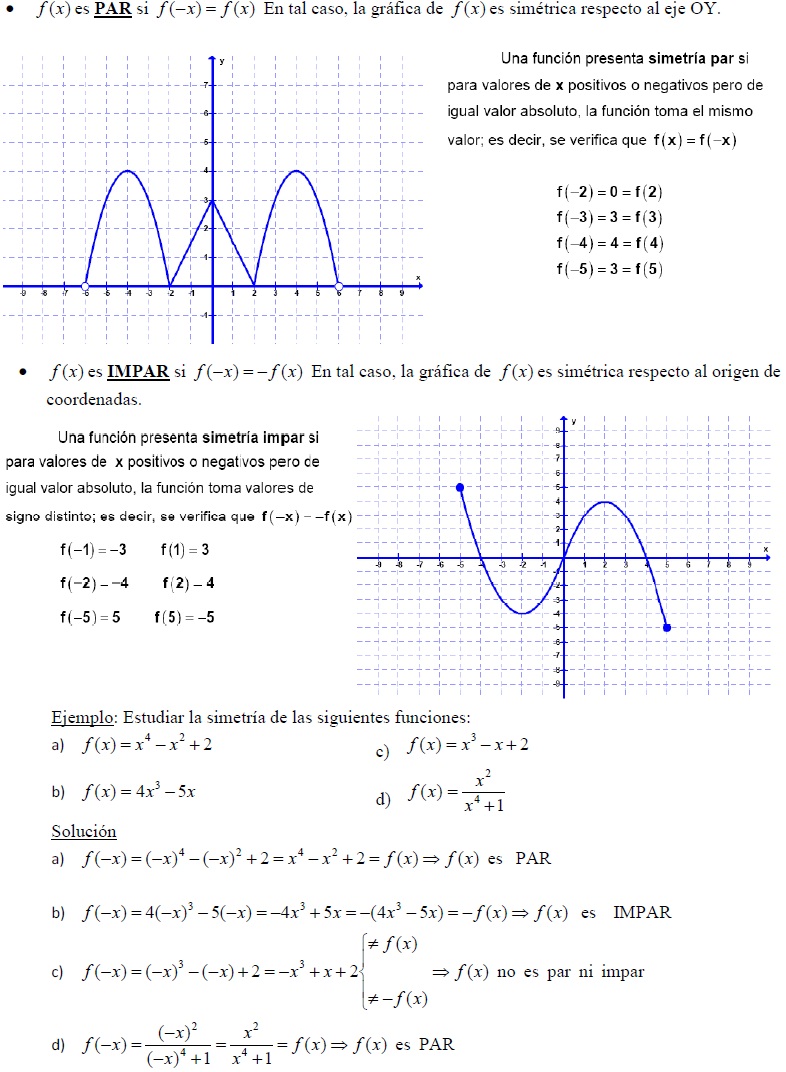
5. Simetría

6. Periodicidad

EJERCICIOS

7. Tendencias, asíntotas

Ejercicios

Transformaciones de funciones

Operaciones con funciones

EJERCICIOS

Composición de funciones

EJEMPLOS

EJERCICIOS

Función inversa

EJERCICIOS

Funciones elementales