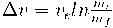Paso 1: Determina o presuposto de Δv

Necesitas estimar o Δv necesario para cada etapa. Como exemplo, empregaremos unha misión non tripulada ata Marte.

Buscamos o Δv de cada manobra e realizamos a seguinte táboa:


Etapa
Δv (m/s)
I
Terra→Órbita terrestre
9400
II
Órbita terrestre→Órbita de Marte
5710
III
Órbita de Marte→Superficie de Marte
≈500


Asumimos que a atmosfera de Marte, pese a ser bastante ténue, nos permitirá realizar un aerofrenado que reducirá moito o Δv da última etapa.


Paso 2: Calcula a masa da última etapa

Nesta misión queremos deixar unha sonda de 3.000 kg orbitando o planeta e pousar un rover de 1.200 kg na superficie marcián.

Para calcular a masa da última etapa, empregaremos a ecuación dos foguetes:

\Delta v=v_eln\frac{m_i}{m_f}

Sabemos a masa final, mf (1200 kg) e o Δv que necesitamos (500 m/s). A velocidade dos gases, ve, dependerá do motor do foguete. No noso caso serán 2400 m/s. Tan solo nos queda despexar na ecuación dos foguetes a masa inicial, mi: 

 m_i=m_fe^\frac{\Delta v}{v_e}

Sustituindo os datos anteriores, obtemos unha masa inicial da última etapa de 1500 kg.


Paso 3: Calcula a masa das outras etapas

Sabendo a masa da última etapa, podemos calcular o resto delas. A masa final da segunda etapa (órbita terrestre→órbita de Marte) será a masa inicial da terceira etapa (1500 kg) máis a masa da sonda que deixaremos na órbita (3000 kg).

Con eses datos, volvemos a sustituir na ecuación dos foguetes e calculamos a masa inicial da segunda etapa. Neste caso, o resultado é 49.000 kg.

Unha vez máis, a masa inicial da segunda etapa será a masa final da primeira etapa. Sustituimos unha vez máis os datos de mf, Δv, ve na ecuación dos foguetes e calculamos a masa inicial. Obtemos que a masa do foguete que debe despegar da Terra son 2.500.000 kg.
Última modificación: luns, 26 de maio de 2025, 5:59 PM