Tema 1. Números racionales e irracionales.
| Sitio: | Aula Virtual |
| Curso: | 4º ESO. MATEMÁTICAS APLICADAS 2020-21 |
| Libro: | Tema 1. Números racionales e irracionales. |
| Impreso por: | Usuario convidado |
| Data: | mércores, 14 de xaneiro de 2026, 2:47 AM |
Descrición

Teoría y ejercicios de números racionales e irracionales.
En cada apartado se os indica la tarea que tenéis que hacer. Pueden ser tareas para entregar o para corregir con calculadora o herramientas digitales. Leed con atención.

- Todo lo que necesitas saber de números enteros.
- Realiza los siguientes ejercicios en tu libreta.
- Corrige los ejercicios anteriores con GeoGebra CAS o con tu calculadora. En tu libreta, debes ir señalando en COLOR ROJO tanto los ejercicios que haces correctamente como los que no. Todas las tareas del aula virtual serán puntuadas a lo largo de cada evaluación hasta un 25% de la nota de evaluación.

OPERACIONES CON POTENCIAS
-
Definición, propiedades y ejercicios de potencias. Descarga este fichero y realiza los ejercicios en tu libreta. Ve comprobando si tu solución es correcta. Si tienes dudas pregunta en clase.
- Realiza este test de Potencias. Debes saber responder correctamente todas las preguntas (100%). Si no es así, debes averiguar cuál es la respuesta correcta y porqué antes de pasar al siguiente punto.
- Aprende a utilizar GeoGebra CAS.
- Realiza en tu cuaderno los ejercicios de la siguiente Ficha. Para corregirlos tienes que utilizar GeoGebra CAS. Si tienes alguna duda pregunta en clase.
OPERACIONES CON POTENCIAS DE 10. NOTACIÓN CIENTíFICA.
- Aprende a usar tu calculadora con la notación científica. Vídeos de ayuda.
- Realiza en tu libreta los siguientes ejercicios. Corrígelos utilizando tu calculadora.

Realiza los siguientes ejercicios en tu cuaderno. Utiliza GeoGebra CAS para ayudarte a corregir.

Conjunto de los números reales
Números naturales
Con los números naturales contamos los elementos de un conjunto (número cardinal). O bien expresamos la posición u orden que ocupa un elemento en un conjunto (ordinal).
El conjunto de los números naturales está formado por:
N= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...}

Números enteros
Los números enteros son del tipo:
 = {...−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 ...}
= {...−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 ...}

Nos permiten expresar: el dinero adeudado, la temperatura bajo cero, las profundidades con respecto al nivel del mar, etc.
Números racionales
Se llama número racional a todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero.


Los números decimales (decimal exacto, periódico puro y periódico mixto) son números racionales; pero los números decimales ilimitados no.
Números irracionales
Un número es irracional si posee infinitas cifras decimales no periódicas, por tanto no se pueden expresar en forma de fracción.
El número irracional más conocido es  , que se define como la relación entre la longitud de la circunferencia y su diámetro.
, que se define como la relación entre la longitud de la circunferencia y su diámetro.
 = 3.141592653589...
= 3.141592653589...
Otros números irracionales son:
El número e aparece en procesos de crecimiento, en la desintegración radiactiva, en la fórmula de la catenaria, que es la curva que podemos apreciar en los tendidos eléctricos.
e = 2.718281828459...
El número áureo,  , utilizado por artistas de todas las épocas (Fidias, Leonardo da Vinci, Alberto Durero, Dalí,..) en las proporciones de sus obras.
, utilizado por artistas de todas las épocas (Fidias, Leonardo da Vinci, Alberto Durero, Dalí,..) en las proporciones de sus obras.

Números reales
El conjunto formado por los números racionales e irracionales es el conjunto de los números reales, se designa por  .
.

Con los números reales podemos realizar todas las operaciones, excepto la radicación de índice par y radicando negativo y la división por cero.
La recta real
A todo número real le corresponde un punto de la recta y a todo punto de la recta un número real.

_____________________________________________________________________Ahora realiza el siguiente test:
Desarrollado por tutores universitarios
|
|
Representación de los números reales sobre la recta
Números decimales


Representación de números irracionales


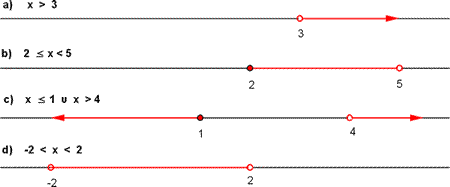
Intervalos y semirrectas

Valor absoluto
