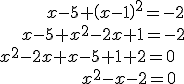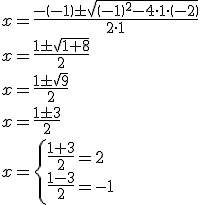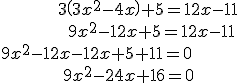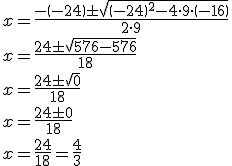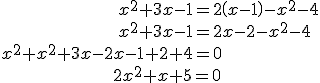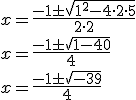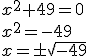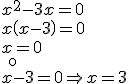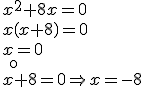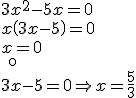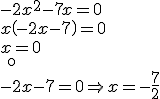Ecuaciones de segundo grado
¿Cómo se resuelve una ecuación de segundo grado?
![]() DEFINICIÓN Una ecuación de segundo grado es una ecuación polinómica en la que, después de ser reducida, el mayor de los grados de los monomios que aparecen es dos. Cualquier ecuación de este tipo se puede expresar de la siguiente forma:
DEFINICIÓN Una ecuación de segundo grado es una ecuación polinómica en la que, después de ser reducida, el mayor de los grados de los monomios que aparecen es dos. Cualquier ecuación de este tipo se puede expresar de la siguiente forma:
![]() ,
,
con ![]() ,
, ![]() y
y ![]() números reales y
números reales y ![]() .
.
Usaremos como ejemplo una ecuación que apareció cuando mientras resolvíamos ecuaciones de primer grado:
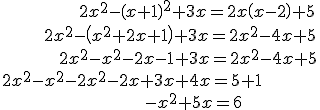
Una vez reducida la ecuación nos quedan tres términos que no podemos juntar, pues no son monomios semejantes. La estrategia que usábamos para ecuaciones de grado 1 no sirve, pero podemos hacer lo siguiente:
| PASO | ESTADO DE LA ECUACIÓN |
| Pasamos todos los términos al mismo miembro. | |
| Multiplicamos ambos miembros de la ecuación por |
|
| Multiplicamos ambos miembros por |
|
| Sumamos |
|
| Deshacemos la identidad notable |
|
| Calculamos la raíz cuadrada de ambos miembros. CUIDADO: El exponente |
|
| Pasamos el |
|
| Pasamos el |
|
| Calculamos las dos soluciones. | 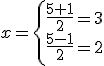 |
Como puedes ver, resolver ecuaciones de segundo grado "a pelo" es un proceso largo y poco intuitivo. La clave está en conseguir una una identidad notable para poder eliminar el exponente ![]() de la
de la ![]() y despejar después con comodidad.
y despejar después con comodidad.
¿Crees que merece la pena repetir un proceso parecido al anterior cada vez que queramos resolver una ecuación de segundo grado? Lo cierto es que no. Lo que haremos será utilizar el lenguaje algebraico para convertir los pasos anteriores en una fórmula que sirva para cualquier ecuación de grado 2. ¿Ves cuantos quebraderos de cabeza te puede ahorrar el álgebra?
Considera una ecuación de segundo grado cualquiera, escrita en la forma ![]() .
.
| PASO | ESTADO DE LA ECUACIÓN |
| Multiplicamos ambos miembros por |
|
| Sumamos |
|
| Deshacemos la identidad notable |
|
| Calculamos la raíz cuadrada de ambos miembros. CUIDADO: El exponente |
|
| Pasamos |
|
| Pasamos |
De ahora en adelante no tendremos que preocuparnos por encontrar identidades notables, aplicaremos directamente la fórmula para resolver cualquier ecuación de segundo grado.
![]() OBSERVACIÓN No es necesario que sepas de dónde sale la fórmula para resolver ecuaciones de segundo grado, pero sí es muy importante que la memorices. Los pasos anteriores aparecen sólo para que veas que no sale de la nada.
OBSERVACIÓN No es necesario que sepas de dónde sale la fórmula para resolver ecuaciones de segundo grado, pero sí es muy importante que la memorices. Los pasos anteriores aparecen sólo para que veas que no sale de la nada.
![]() ALGORITMO Para resolver una ecuación de segundo grado:
ALGORITMO Para resolver una ecuación de segundo grado:
Reducimos la ecuación hasta que tenga la forma ![]() .
.
Aplicamos la fórmula ![]() .
.
Fíjate en los siguientes ejemplos:
| ECUACIÓN 1 | ECUACIÓN 2 | ECUACIÓN 3 |
|
Primer paso: Reducimos la ecuación.
Segundo paso: Identificamos
|
Primer paso: Reducimos la ecuación.
Segundo paso: Identificamos
|
Primer paso: Reducimos la ecuación.
Segundo paso: Identificamos
No tiene solución.
|
¿Cuántas soluciones tiene una ecuación de segundo grado?
En la fórmula para resolver ecuaciones de segundo grado aparece una raíz cuadrada. El número de soluciones depende del signo del radicando.
![]() ALGORITMO Dada una ecuación de segundo grado,
ALGORITMO Dada una ecuación de segundo grado, ![]() , con
, con ![]() ,
, ![]() y
y ![]() números reales y
números reales y ![]() , dicha ecuación puede tener:
, dicha ecuación puede tener:
Dos soluciones, si ![]() .
.
Una solución, si ![]() .
.
Ninguna solución, si ![]() .
.
![]() suele recibir el nombre de discriminante.
suele recibir el nombre de discriminante.
En los ejemplos anteriores puedes ver cada una de las tres situaciones.
Ecuaciones de segundo grado incompletas
La fórmula para resolver ecuaciones de segundo grado es muy útil, pero no siempre es necesaria. Existen ecuaciones de grado 2 con las que compensa seguir otra estrategia. Son aquellas en las que no aparece término de grado 1 o término independiente.
ECUACIONES DE SEGUNDO GRADO SIN TÉRMINO DE GRADO 1
Podemos despejar la incógnita y calcular una raíz cuadrada. Fíjate en los ejemplos:
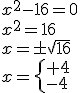 |
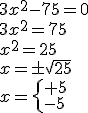 |
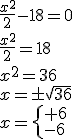 |
No tiene solución |
ECUACIONES DE SEGUNDO GRADO SIN TÉRMINO INDEPENDIENTE
Podemos sacar factor común y transformar la expresión en un producto igualado a cero. Fíjate en los ejemplos:
|
SOLUCIONES:
|
SOLUCIONES:
|
SOLUCIONES:
|
SOLUCIONES:
|