Ecuaciones de primer grado

¿Cómo se resuelve una ecuación de primer grado?

icono_definicion DEFINICIÓN Una ecuación de primer grado es una ecuación polinómica en la que, después de ser reducida, el mayor de los grados de los monomios que aparecen es uno.

OBSERVACIÓN Una ecuación de primer grado puede no parecerlo antes de ser reducida. Es importante completar las operaciones y transponer términos antes de llegar a una conclusión sobre el tipo de ecuación que tenemos entre manos.

Fíjate bien en las siguientes ecuaciones. La diferencia entre las expresiones de partida de una y de otro es mínima (sólo cambia un número) pero la forma de resolver una y otra es muy diferente. Ejemplos:

ECUACIÓN DE PRIMER GRADO QUE PARECE DE SEGUNDO GRADO

ECUACIÓN DE SEGUNDO GRADO

Si operamos y transponemos:

eq1_p4_c1b

Si operamos y transponemos:

eq2_p4_c1b

Como puedes ver, para resolver la ecuación de primer grado es suficiente con operar y transponer, aislando (despejando) la incógnita y los números. La segunda ecuación se queda de momento sin resolver. Volveremos a trabajar con ella cuando estudiemos las ecuaciones de segundo grado.

ALGORITMO Para resolver una ecuación de primer grado en una variable, nos limitaremos a realizar todas las operaciones indicadas en los dos miembros de la ecuación, reduciéndolos tanto como podamos, y transponer los términos resultantes para dejar la incógnita aislada en uno de los miembros.

Debido al rigor con el que tienen que realizarse las operaciones matemáticas, es conveniente establecer un orden de trabajo a la hora de resolver una ecuación de este tipo:

Primer paso: Quitamos paréntesis (Propiedad distributiva de la multiplicación).
Segundo paso: Quitamos denominadores. La clave está en hacer que todos los términos de la ecuación tengan denominador común y multiplicar después ambos miembros por dicho denominador.
Tercer paso: Despejamos la incógnita reduciendo y transponiendo términos según sea conveniente.

El primer paso y el segundo pueden no ser necesarios si no aparecen paréntesis o denominadores en la ecuación.

En la siguiente tabla encontrarás ejemplos, explicados paso a paso, de todas las posibles situaciones.

ECUACIÓN SIN PARÉNTESIS Y SIN DENOMINADORES
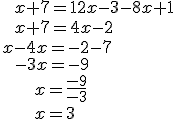	Sólo tienes que sumar o restar monomios y transponer. Recuerda que no es obligatorio llevar la incógnita al primer miembro. CUIDADO: Cuando un número pasa a otro miembro multiplicando o dividiendo, su signo no cambia. Fíjate en los últimos pasos del ejemplo.
ECUACIÓN CON PARÉNTESIS Y SIN DENOMINADORES
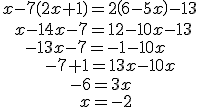	Para quitar los paréntesis no tienes más que aplicar la propiedad distributiva. CUIDADO: Presta especial atención a los signos. El número que multiplica a lo que está entre paréntesis (y su signo) afecta a todos los monomios que están entre dichos paréntesis.
ECUACIÓN SIN PARÉNTESIS Y CON DENOMINADORES
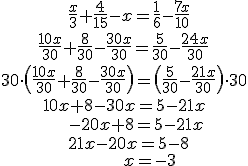	Para encontrar el denominador común sólo tienes que calcular el mínimo común múltiplo de los denominadores que aparezcan. En el primer ejemplo es el y en el segundo ejemplo el . En el primer ejemplo puedes ver escrito lo que se hace para eliminar denominadores: Se multiplican ambos miembros de la ecuación por el denominador común. Lo normal es no escribir esos productos, sino eliminar directamente los denominadores sin escribir nada, asumiendo que el lector entiende lo que se hace, como en el segundo ejemplo. Una vez calculado el denominador común, puedes optar por escribir cada término de la ecuación como una fracción independiente, como en el primer ejemplo, o poner todos los términos de un mismo miembro sobre el mismo denominador, como en el segundo ejemplo. CUIDADO: Cuando quites los denominadores o cuando pongas varios términos de la ecuación sobre el mismo denominador, presta especial atención a los signos. Ten en cuanta que el signo que precede a una fracción afecta a todos los monomios que aparezcan en el numerador. En el segundo ejemplo, fíjate en lo que pasa con el signo del del primer miembro en el segundo paso.

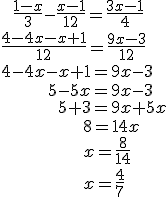ECUACIÓN CON PARÉNTESIS Y CON DENOMINADORES
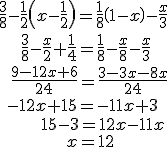	En estos ejemplos aparece todo lo que te puedes encontrar en una ecuación de primer grado. Haz las cuentas con calma, respeta el orden y las propiedades de las operaciones. Si te fijas, al mismo tiempo que se quitan los denominadores, se aprovecha para hacer alguna operación. No es obligatorio, hazlo sólo si te manejas las ecuaciones con soltura. En el segundo ejemplo, después de quitar paréntesis, se simplifica una de las fracciones que resulta. No es obligatorio para resolver la ecuación, pero puede facilitar las cuentas en muchos casos. CUIDADO: A riesgo de ser pesado, ten mucho cuidado con el signo cuando trabajes con paréntesis y denominadores.

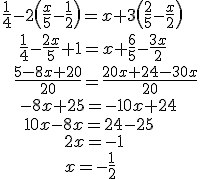Vídeotutorial

Puedes ver la resolución de una ecuación de primer grado con paréntesis y denominadores en el siguiente videotutorial.

Piensa...

Fíjate en lo que pasa al intentar resolver las dos siguientes ecuaciones:

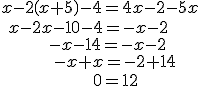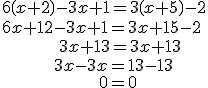Lo que sucede es que esas igualdades no son realmente ecuaciones, ya que no establecen ninguna condición sobre la variable. Después de reducirlas, las variables "desaparecen" y sólo queda una igualdad entre números, que puede ser falsa, como en la primera igualdad, o cierta, como en la segunda.

En el primer ejemplo podríamos decir que la igualdad inicial es cierta cuando , pero como eso es imposible, diremos que NO TIENE SOLUCIÓN.

En el segundo ejemplo podríamos decir que la igualdad inicial es cierta cuando , pero como eso es siempre cierto, diremos que CUALQUIER NÚMERO ES SOLUCIÓN.

icono_observacion OBSERVACIÓN Puede parecer una tontería, pero no es lo mismo decir "tiene infinitas soluciones" que "cualquier número es solución". Por ejemplo, hay infinitos valores que hacen cierta la ecuación , pero no cualquier par de valores es solución.

Comprueba si las siguientes expresiones son identidades o ecuaciones. Indica si tienen una solución, ninguna o si cualquier número es solución. Pulsa el botón para comprobar tus respuestas.