Monomios

¿Qué es un monomio?

Cuando empiezas a estudiar un idioma nuevo no tienes que aprenderte todas las palabras del diccionario. Al principio te limitas a manejar las estructuras más simples y un vocabulario básico. Con el lenguaje algebraico haremos exactamente lo mismo, nos limitaremos primero a las expresiones algebraicas más sencillas y las operaciones que podemos hacer con ellas.

icono_definicion DEFINICIÓN Un monomio es el producto de un número conocido (coeficiente) por uno o varios valores desconocidos, representados por letras (parte literal). El grado de un monomio es el número de factores que forman su parte literal (la suma de los exponentes de las letras).

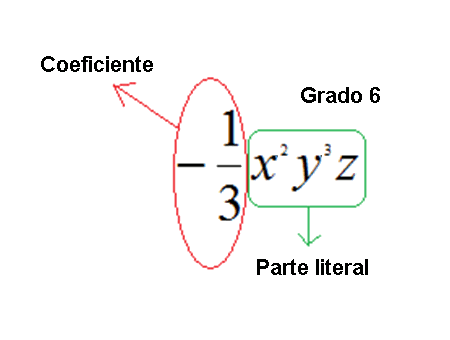
dibujo_monomio

OBSERVACIÓN El coeficiente del monomio incluye el signo y la parte literal incluye los exponentes de cada una de las variables.

icono_notacion NOTACIÓN Habitualmente daremos a los monomios (también a los polinomios) un "nombre". La idea es poder hacer referencia a ellos sin tener que escribir el monomio completo. Los nombres de los monomios (y de los polinomios) tendrán dos partes: Una letra mayúscula (lo normal es usar desde la en adelante) y las variables que forman parte del monomio, entre paréntesis. Por ejemplo:

, ,

Con la notación anterior resulta más sencillo hacer referencia al valor numérico de un monomio. El nombre que escogemos está acompañado de las variables del monomio, así que si queremos referirnos a un valor numérico en concreto no tenemos más que escribir el nombre del monomio cambiando las variables por el valor que corresponda. Por ejemplo:

Dado el monomio , en lugar de escribir "valor numérico de para , ", escribiremos simplemente . En este caso:

DEFINICIÓN Dos monomios se dicen semejantes si tienen la misma parte literal, es decir, si sus partes literales están formadas por los mismos factores. No es relevante si los factores aparecen en el mismo orden. Por ejemplo, los monomios y son semejantes, pero los monomios y no lo son.

Dos monomios se dicen opuestos si son semejantes y tienen coeficientes opuestos. Por ejemplo, y son monomios opuestos.

¿Qué operaciones podemos hacer con monomios?

En la siguiente tabla tienes explicaciones y ejemplos para todas las operaciones que podemos hacer con monomios.

SUMA Y RESTA DE MONOMIOS
SI SON SEMEJANTES	SI NO SON SEMEJANTES
Podemos sacar factor común (la parte literal) y sumar o restar los coeficientes. Ejemplos:	Tenemos que dejar la operación indicada. Ejemplos:
MULTIPLICACIÓN DE MONOMIOS
Aplicamos la propiedad asociativa de la multiplicación y hacemos el producto de coeficientes y de las variables por separado. Es importante usar correctamente la regla de los signos y las propiedades de las potencias (ésta última para la multiplicación de las partes literales). Ejemplos:
DIVISIÓN DE MONOMIOS
Al igual que para la multiplicación, dividimos los coeficientes entre ellos y las partes literales entre ellas. El cociente de dos monomios puede no ser un monomio. Ejemplos: (No es un monomio)