Probabilidade
| Website: | Aula virtual do espazoAbalar |
| Kurs: | Os problemas: o motor das matemáticas |
| Buch: | Probabilidade |
| Gedruckt von: | Usuario convidado |
| Datum: | Sonntag, 1. März 2026, 20:24 |
Beschreibung
Resumo de teoría de probabilidade e exercicios resoltos.
Dado un experimento aleatorio ,é dicir, un experimento repetible de resultado incerto.
Podemos calcular a probabilidade de un suceso A da seguinte maneira:
Exemplo: se o experimento aleatorio consiste en lanzar un dado de seis caras iguais:
a probabilidade de obter un dous é
a probabilidade de obter un número impar é
Chamamos sucesos elementais a cada un dos resultados do experimento aleatorio. O conxunto de sucesos elementais forman o espacio mostral E.
No exemplo E={1,2,3,4,5,6}
Se lanzamos unha moeda o espazo mostral será E={CARA,CRUZ}
Se lanzamos dúas moedas o espazo mostral será E={CARA-CARA,CARA-CRUZ,CRUZ-CRUZ,CRUZ-CARA}, catro resultados posibles cada un deles igualmente probable.
Neste caso a probabilidade de ter unha cara e unha cruz será:

Xa que temos dúas xogadas nas que sacamos unha cara e unha cruz : CARA-CRUZ e CRUZ-CARA.
Podemos crear novos sucesos combinando sucesos elementais, para iso usaremos operacións lóxicas.
As palabras clave son E, OU e NON.
Dados dous sucesos A e B, definimos os seguintes sucesos:
A unión B (A OU B): suceso consistente en que ocurre o suceso A OU ocorre o suceso B (OU os dous ocorren)
A intersección B (A E B): suceso consistente en que ocorre o suceso A e tamén o suceso B.
Suceso contrario NON A: suceso consistente en que ocorre calquer cousa menos A (non ocorre A).
Se de novo tiramos un dado, podemos pensar no suceso P="sae par" como a unión dos sucesos A2="sae un 2", A4=" sae un 4", A6=" sae un 6".
A forma de expresalo sería: A =A1 OU A2 OU A3,
Como ves existen diferentes formas de chamarlle aos sucesos, básicamente son tres:
- Póñense entre comiñas cando explicamos literalmente en que consiste o suceso.
- Poñense entre chaves cando usamos o resultado suceso {2,4,6}
- Denótanse por unha letra ou varias letras que recorden o que pasa suceso P ="sae par".
O suceso contrario tamén e moi útil para expresar (e calcular a probabilidade) dalgúns sucesos, por exemplo:
o suceso B={2,3,4,5,6} pódese pensar como Non C, sendo C={1}
Fórmula da Probabilidade total:
Relaciona a probabilidade da unión coa da intersección de sucesos.
Cando sumamos a probabilidade de A e a de B (P(A)+P(B)) sumamos dúas veces a probabilidade do suceso intersección P(A E B) por que temos que restala unha vez para ter P(A OU B)
Cando os sucesos A e B son incompatibles, isto é: se sucede un o outro non pode suceder, á formula queda máis sinxela.
Como o suceso A E B é imposible, ten probabilidade cero e desaparace da fórmula:
A situación sería a seguinte A e B "non se tocan"
Lei da multiplicación:
A e B son sucesos independentes cando o feito de que ocorra un non inflúe na probabilidade de que ocorra o outro.
Exemplo 1: Se tiro dúas moedas o feito de que a primeira sexa cara non inflúe na probabilidade de que a segunda sexa cara, logo os resultados dos lanzamentos son sucesos independientes.
Exemplo2: Se tiro un dado o suceso "sae par" e o suceso "sae 4" non son independentes.
SE A e B independentes
Probabilidade do suceso contrario:
Gráfico de conxuntos
Imaxina que na clase de matemáticas un 30% dos estudantes xoga a xadrez, un 50% xoga a parchís e un 20% xoga a xadrez e tamén a parchís.
Resulta bastante aceptable que se escollemos un estudante ao chou, a probabilidade de que xogue a xadrez sexa 30%; xa que esta é a proporción de estudantes que gostan do xadrez.
Se escollemos un estudante ao chou, cal é a probabilidade de que xogue o xadrez ou o parchís?, neste caso necesitamos usar a fórmula da probabilidade total:
Recorda que
Neste caso resulta moi útil o gráfico de conxuntos (chamado diagrama de Venn), no que representamos os conxuntos do problema e colocamos as cantidades correspondentes.
Agora, coñecendo a porcentaxe que representa cada parte disxunta, xa podemos responder, doadamente, calquera cuestión.
Que porcentaxe da clase xoga somentes a un dos dous xogos? Ou, dito doutro modo: se escollo a un estudante ao azar, cal é a probabilidade de que so xogue a un dos xogos?.
Collendo bólas dunha urna
Temos agora unha urna chea de bólas de diferentes cores. Por exemplo: 4 Brancas, 4 Negras e 2 Verdes.
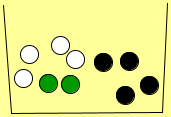
Agora remexemos ben e sacamos 2 bólas. Resulta moi práctico para analizar a situación, pensar que sacamos unha bóla e despois outra (en realidade tanto ten sacar dúas ao mesmo tempo que unha e despois outra).
Os casos posibles ou o espazo mostral será: {branca-branca,branca-verde,branca-negra,verde-verde,verde-branca,verde-negra,negra-negra,negra-branca,negra-verde}.
Parece bastante razoable pensar que non todos os casos son igualmente probables, xa que as bólas verdes están en clara minoría terán que sair con menor frecuencia.
Facemos unha árbore para asignar probabilidades coa regra de Laplace:
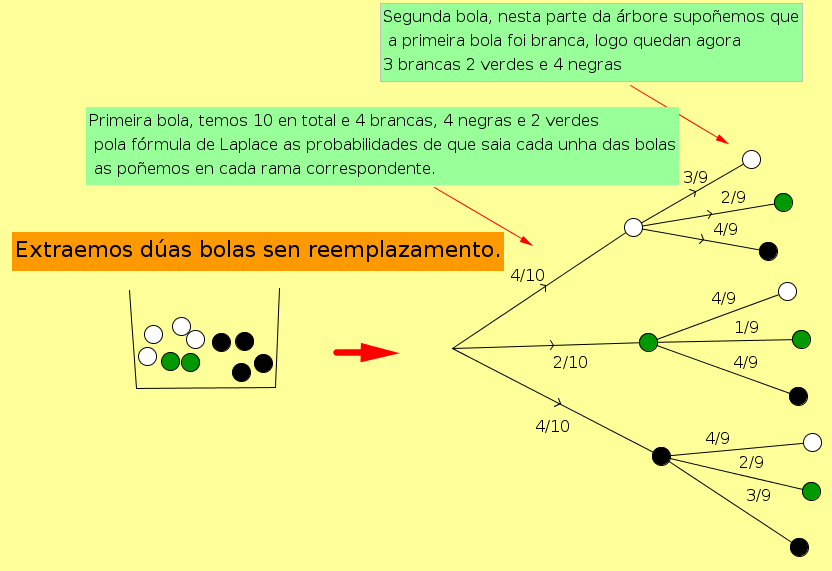
Agora coa árbore montada, podemos calcular a probabilidade de calquera suceso elemental (resultado) e por suposto de calquera suceso (conxunto de resultados).
Probabilidade de dúas verdes: P(verde-verde)=P(primeira verde)xP(segunda verde)=2/10x1/9=2/90=1/45.
Outros exemplos na propia árbore:
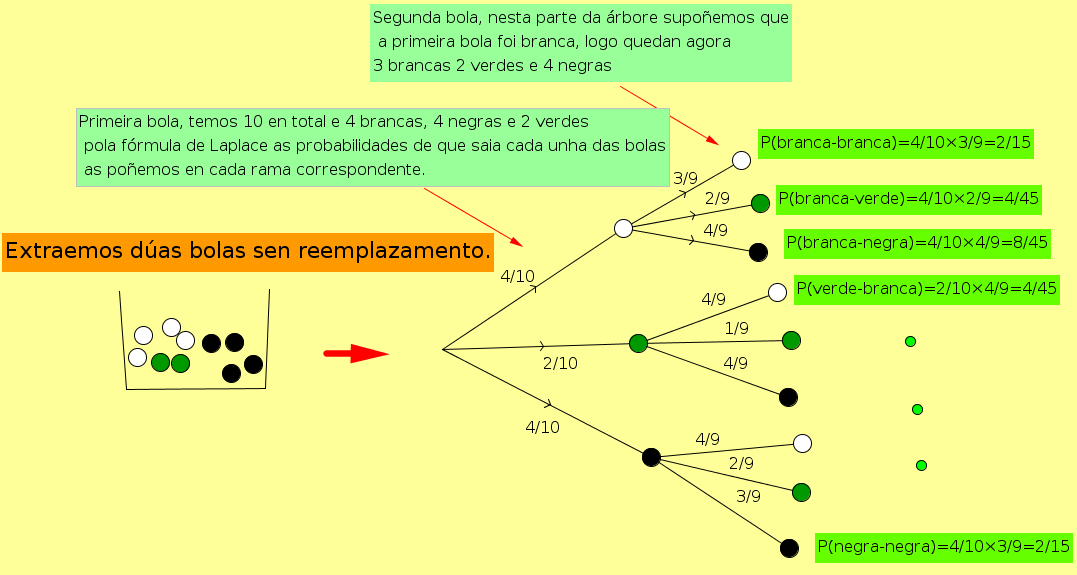
Tarefa: Calcula a probabilidade de obter dúas bolas da mesma cor (tes que sumar a probabilidade dos resultados branco-branco, verde-verde, negro-negro).
Diagrama de árbore
Imaxina que lanzo dúas moedas.Cal é o espazo mostral? Ou, dito doutro xeito: cales son os resultados que podo obter?
Aos experimentos coma este, nos que facemos varios sorteos, chamámolos experimentos compostos.
Este é o espacio mostral E= {(CARA, CARA),(CARA,CRUZ),(CRUZ,CARA),(CRUZ,CRUZ)}. Aquí, os resultados son pares xa que lanzamos dúas moedas.
Resulta especialmente útil facer unha árbore para analizar os posibles resultados. En cada rama da árbore poñemos a súa probabilidade.
Agora para calcular a probabilidade dun suceso elemental(resultado do experimento composto), chega con multiplicar a probabilidade das súas ramas na árbore.
Por exemplo:
Este mesmo resultado obtémolos coa fórmula de Laplace:
Cal será a probabildade de obter unha cara polo menos?
Neste caso podemos utilizar o suceso contrario, xa que resulta moi práctico:
Tarefa: Calcula doutro xeito a probabilidade anterior (podes usar a fórmula de Laplace).